|
|
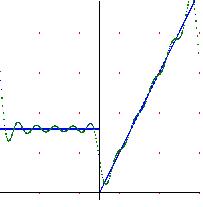
Convergencia de las series de Fourier al valor medio del salto en puntos con discontinuidades de salto.
|
Esta sección es bien corta, veremos en ella el comportamiento de las Series de Fourier en funciones con discontinuas de salto.
Exactamente, el Teorema de Dirichlet nos asegura que en los puntos donde ocurren las discontinuidades de salto, la Serie de Fourier converge al valor médio del salto.
Veremos también el llamado Fenómeno de Gibbs, el cual nos cual dice que cerca de una discontinuidad de salto, la Serie de Fourier se dispara un 9% del valor del salto.
Teorema de Dirichlet
Sea f una función contínua salvo en un punto\( x_0 \in [a, b]\). Supongamos que existen
\( f(x_0^+)=\lim_{t\to 0^+} f(x_0+t)\)
y
\( f'(x_0^+)=\lim_{t\to 0^+} \frac{f(x_0+t) - f(x_0)}{t} \)
Entonces la Serie de Fourier converge al punto médio del salto, es decir
\( \lim_{N\to \infty}S_Nf(x_0) = \frac{f(x_0+t) - f(x_0)}{t} \)
Veremos ahora el llamado Fenómeno de Gibbs
Teorema (Fenómeno de Gibbs)
Sea f como en el Teorema anterior y sea \( S_Nf(x_0) \) la Serie de Fourier de f cerca \( x_0 \in [a, b]\). Entonces la serie se dispara con un valor de aproximadamente
el 9% del valor del salto de f, es decir:
$$ \lim_{t\to 0^+} \left [ \lim_{N\to \infty} (\sup_{x_0 \in (x, t)} S_Nf(x)) \right ] \cong S_Nf(x_0^+)+0.09(f(x_0^+)-f(x_0^-)) $$



