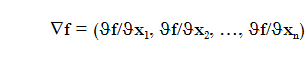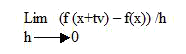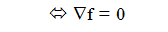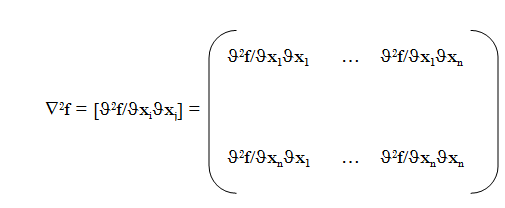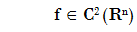We will in this sections see problems of kind
min f (x)
Subject to
gi (x) = 0
With
gi: Rn → R
f: Rn → R
x ∈ Rn
where now, both the objective function and constraint functions are functions
differentiables .
as we have mentioned, the problem may be understodd how a special extended maximum and minimal value problems.
Lets f continuous and
differentiable function
The
Gradient of f is defined as
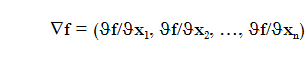
we will also reffers it as grad f(x)
This is, the gradient is a vector formed for all partial derivates of f.
Also we have the concept
Directional derivate
Given a vector v, the directional derivate at the direction vector v is defined as
Df(x)v = df(x+tv)/dt evaluated at t=0.
Also
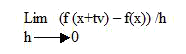
The following theorem assures the existence of all directional derivatives in the case of
diferentiable functions
Theorem (Directional derivate existence in differentiable functions)
Lets

differentiable function, then there exist all directional derivatives and the derivative at a point x in direction v is given by the scalar product of the gradient of f by vector v:
Df(x)v = <grad f(x) . v >
We can interpret the directional derivative in direction v as the rate of change of function in the direction of v
This is interesting for our problem because given a point, we need to know in which direction the function is increasing or decreasing and specially we are interested increasing or decreasing direction faster.
The following Theorem answers these questions
Theorem
If grad f(x) ≠ 0, then the vector grad f(x) points to faster increasing direction of the function f
In other words, if we know in which direction the function f grows faster, we must look in the direction of the vector grad f(x).
Similarly, the direction in which the function decreases faster than the de -grad f(x).
This gives us an idea of an algorithm, given a point (x, f (x)), using numerical methods we can calculate the vector grad f (x) and iterate in this direction (ascending or descending order according to our problem is a maximize or minimize problem).
The following theorem say about
locale extreme of functions points.
Theorem (Minimum local - Convexity relation)
Lets f as before
f has a
local minimum at x
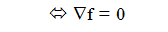
and f is
convex in a neighborhood of x
Note It ss possible to formulate an analogous theorem for the concavity case - local Maximum relation.
Now, given a point where grad f(x) = 0. How to know if this is a local minimum, local maximum or a chair point? The rest of this section will treat about this question
Lets f two times differentiable, the
Hessian matrix is defined as
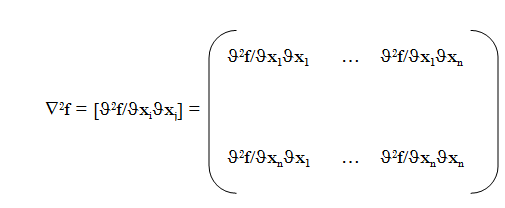
Theorem (Locale extreme characterization)
Lets
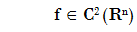
and x a point where grad f(x) = 0, then
a) If the matrix
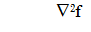
is
positive defined x is a local minimum of f.
b) If is
negative definided
then x is a local maximum of f.
c)
if it is not positive defined and nor negative defined,
then x is a
chair pointof f.
Theorem (Characterization of convexity throught the Hessian)
Lets
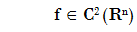
f is
convex if and only if
the matrix
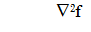
is positive defined
then if f is f
convex
in all points of region S and has
local minimum at x, then x is optimal solution
because it will be a
global minimum .
The convexity of a function only ensures the continuity of the function.
Therefore we can not speak generally of the gradient and Hessian matrix alone.
Instead, in the next section will define the subgradient, which makes the gradient function
at not
differentiable functions case
(in fact, the subgradient is the gradient when the function is differentiable)
Now we can see the complexity of a problem of nonlinear programming. In the case of
convex functions it is much easier since local minimum become global minimum.