Se llama par encajado de Fehlberg de orden n+1,n a un método doble formado por la unión de dos métodos de Runge-Kutta m1, m2 con órdenes n+1 y n respectivamente y cuyas matrices A de sus tableros de Butcher coinciden. Lo explicamos con un poco mas de detalle más abajo.
La idea del par encajado de Fehlberg es que llegado a un nodo utiliza el método de mayor orden (n+1) para estimar el error y el de menor orden (n) para aceptar el paso y avanzar. Los pares encajados de Fehlberg reciben el nombre en la forma NOMBRE_DEL_METODO_ORDEN1_ORDEN2. Por ejemplo el método NEW65 quiere decir que usa un Runge-Kutta de orden 6 para estimar y un Runge-Kutta de orden 5 para avanzar.
Existen otros métodos llamados de Dorman-Prince en los cuales se avanza con el método de mayor orden y se estima con el de menor orden. Un ejemplo de este es el DOPRI54
Ya habíamos comentado que los métodos de Runge-Kutta pierden precisión rápidamente si estamos integrando funciones con derivadas 'grandes'. Lo interesante de un par encajado es que en cada uno de los nodos van rectificando el tamaño del paso y si el error estimado es mayor que un cierto valor que definimos a priori y que llamamos Tolerancia del método o simplemente
Tolerancia entonces el paso se repite con un h mas pequeño.

Teoría en extensión
Un par encajado de Fehlberg toma dos métodos
de Runge Kutta m1 y m2, el primero con orden n+1 y el segundo con orden
n y m1 y m2 son tales que la matriz A de sus tableros de Butcher son
la misma para los dos.

Los pares encajados de Fehlberg funcionan de la siguiente manera: elegimos a priori un parámtro llamado tolerancia, y avanzamos un paso de longitud h con cada uno de los métodos. La idea es suponer el valor dado por el método m1, s1 como solución verdadera y la del método m2, s2 como aproximación.
Ahora calculamos la diferencia entre s1 ys2, si dicha diferencia es menor que la tolerancia damos por bueno el paso y pasamos al siguiente, en cambio, si la diferencia es mayor que la tolerancia entonces volvemos a calcular el paso con un tamaño de paso h1<h, es decir, acortamos el paso para que el error sea menor que la tolerancia.
En el caso de aceptar el paso, también recalculamos el tamaño h1 para el paso siguiente, con h1>h. Lo que se busca con esto es que el tamaño del paso vaya variando en función de la estimación obtenida, de manera que
1) Ahoremos tiempo y coste de máquina en cada paso, tomando un paso más corto allí donde es necesario.
2)Prevenir rechazos por la razón apuntada en el punto anterior
Hacemos un cuadro completo y resument del funcionamiento
Funcionamiento del par encajado de Fehlberg:
Tomamos un tamaño de paso h, y elegimos un valor
máximo aceptable del error que llamaremos Tolerancia.
1) Calculamos la solución, s1, en el paso n con el método m1.
2) Calculamos la solución, s2, en el paso n con el método m2.
3) Tomamos la solución aportada por el método
m2, s2, como la solución real.
4) Calculamos
|s1 - s2| = Estimacion
5a) Si estimación < Tolerancia entonces, tomamos
la solución aportada por el método m2 y avanzamos
hacia el paso siguiente haciendo h un poco más grande.
5b) en caso contrario, rechazamos el resultado obtenido, tomamos un tamaño de paso h1<h y volvemos al paso 1).
Es decir, avanzamos con el método de menor orden y estimamos el error con el método de mayor orden.
Es importante resaltar que tanto si el paso se acepta como si se rechaza el par encajado recalcula el tamaño del paso h.
Estos métodos son muy adecuados en aquellos casos en los que la derivada de la función a integrar sufre muchos cambios ya que el par encajado de Fehleberg va rectificando el tamaño del paso en cada uno de los nodos de tal manera que cuando la derivada es grande, avanzan con un paso más pequeño y por contra, cuando la derivada es pequeña aumentan automáticamente el tamaño del paso, permitiendo con ello un ahorro en el coste de las operaciones.
Como los pares encajados recalculan el tamaño del paso? La respuesta a esta pregunta es que depende un poco del método, pero una fórmula general para un par encajado de orden n y m puede ser la siguiente
h' = 0.9 h min {5, (tolerancia/estimacion)
1/n}
Nota importante: La fórmula anterior es genérica, no es aplicable exactamente igual a todos los pares encajados, si bien en los ejemplos aquí probados ha funcionado bien.
Para terminar, vamos a ver un ejemplo con muchos cambios en la derivada en el intervalo [0, 1], por ejemplo el problema
y' = sin100x
y(0) = - 1/100
Cuya solución es obviamente y(x) = (-1/100) cos 100x.
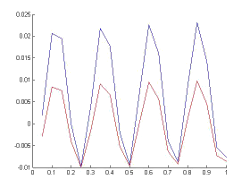
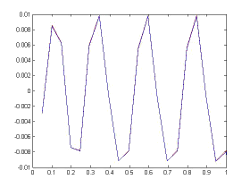
Si tomamos el método R/K clásico de orden 4 con 20 pasos (h=0.05) y el par encajado de Fehlberg New65f (se trata de un método cuyo par encajado está formado con por un método Runge-Kutta de orden 6 para estimar y otro Runge-Kutta orden 5 para avanzar) con 13 pasos (es decir un paso medio de 0.76. Si dibujamos
en rojo la gráfica de la función y
en azul los valores obtenidos por cada uno de estos métodos, los Gráficos que obtenemos son
|
|
Rk4: Obsérvese el incremento del error en los puntos donde cambia la derivada, es decir, en puntos correspondientes a máximos y minimos locales.
|
|
|
|
New65f: Obsérvese que la grafica de la funcion y el método son indistinguibles ya con 22 pasos: el método es capaz de seguir a la función con solo este número de pasos.
|
|
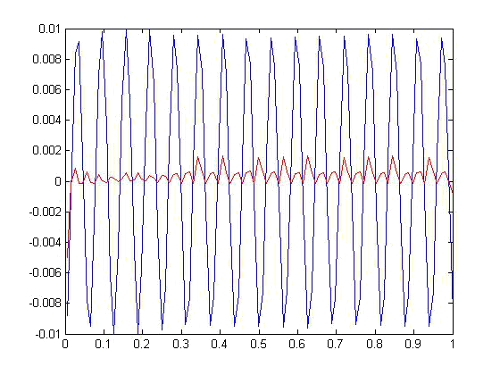
Vamos a tomar ahora el mismo problema solo con el par encajado New65f, pero ponemos ahora una tolerancia de 1.5 x10-7, es decir pedimos más precisión, en concreto pedimos que el tamaño de paso medio sea del orden de 0.01, hacemos el gráfico en azul los valores del método y en rojo la varianza del tamaño del paso en cada nodo, vease como el par encajado disminuye el tamaño del paso en los puntos donde la derivada es mayor.