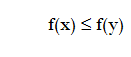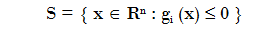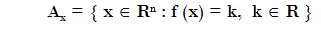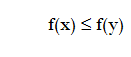Un problema de programación no lineal es un problema de la forma
min f (x)
Sujeto a
gi (x) = 0
Con
gi: Rn → R
f: Rn → R
x ∈ Rn
El problema es muy distinto del que teníamos en el caso lineal donde a través de métodos de algebra lineal podíamos resolver el problema.
En el caso no lineal nuestro trabajo será mucho más complejo y profundo, pues evoca conceptos como "continuidad", convexidad o diferenciabilidad y
abarca varios campos del análisis, y de la topología.
En el caso de tanto tener
diferenciabilidad tanto en la función objetivo como las funciones de restricciones el problema se puede plantear a algo parecido a un problema extendido de máximos y mínimos.
Sea la región factible
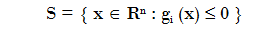
Y sean los conjuntos de nivel de la función
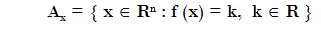
El conjunto factible tal como viene dado en nuestro problema es un conjunto de la forma
O también podría no estar acotado y adoptar una forma como

Y los conjuntos de nivel de la función objetivo
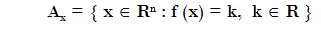
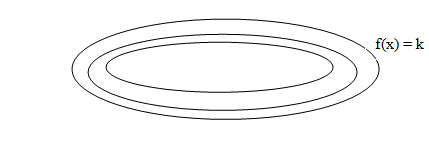
En general, el conjunto de restricciones delimita una región de R
n. Haremos hipótesis sobre esta región (con frecuencia de topológicas) sin prestar tanta atención a las funciones g
i en si mismas.
En primera instancia, sabemos que toda función continua en un compacto está acotada (superior e inferiormente)
, este Teorema junto con el axioma 13 de los números reales que dice que
todo conjunto de números reales acotado superiormente (inferiormente) tiene extremo superior (inferior)
nos asegura la existencia de un valor óptimo para nuestro problema.
Por tanto en el caso de que tengamos compacidad en el conjunto de restricciones tenemos un teorema de existencia y podemos asegurar que existe un punto y, de la región factible, S tal que para todo x de S se tiene