Veremos en esta sección una aplicación de solución práctica de un típico problema de maximización. A veces lo dificil es llegar a plantear el problema de programación lineal, una vez planteado, usaremos los métodos aprendidos en la teoría: con el método del simplex y método de las dos fases.
Comenzamos con el enunciado de un problema de optimización.
Problema de programación lineal
Una compañía minera produce lignito y antracita.
Por el momento, es capaz de vender todo el carbón producido, siendo la ganancia por tonelada de lignito y antracita de 4 y 3 unidades monetarias, respectivamente. El procesado de cada tonelada de lignito requiere 3 horas de trabajo de la máquina de cortar carbón y otras 4 horas de la de lavado.
Por otra parte, el procesado de una tonelada de antracita requiere para las mismas tareas 4 y 2 horas, respectivamente.
El tiempo disponible diariamente para cada una de estas actividades es de 12 y 8 horas, respectivamente. Además, se desea producir diariamente al menos 4 toneladas de carbón.
1) Plantear el problema de programación lineal para determinar el número de toneladas de lignito y antracita que deben producirse diariamente con el fin de maximizar la ganancia.
2) Usar el algoritmo del simplex para resolver el problema por el método de las dos fases. Comenzamos entendiendo este largo enunciado. Para ello construimos unas tablas.
La primera de ellas es la de costes, o en este caso, es una tabla de Ganancias.
| Material | Ganancia produdida
(unidades monetarias/Tn) |
| Lignito | 4 |
| Antracita | 3 |
| Material | Horas de cortado (por Tn) | Horas de lavado (por Tn) |
| Lignito | 3 | 4 |
| Antracita | 4 | 2 |
Unido a esta tabla, tenemos la restricción del tiempo disponible diario para cada máquina
| Proceso | Horas disponibles diariamente |
| Lavado | 8 |
| Cortado | 12 |
y finalmente, tenemos el objetivo de producir al menos 4 Toneladas diarias de carbón.
Con estos datos, tenemos lo que necesitamos para plantear el problema de programación lineal.
Procedemos de la siguiente manera:
Sean
x1=Toneladas de lignito producidas
x2=Toneladas de antracita producidas
Lo que queremos es maximizar la ganancia, es decir, maximizar la función 4x1+3x2, ya tenemos la función objetivo, ahora construimos las restricciones.
Comenzamos por el proceso de lavado, obsérvese que para cada día tenemos que
3x1+ 4x2 ≤ 12
Ya que para cada día el número disponible de horas de lavado es 12.
Análogamente para el cortado tenemos que
4x1+ 2x2 ≤ 8
Ya que 8 es el número de horas disponibles para la máquina de cortado.
Finalmente, la última de las restricciones es la de nuestro objetivo de toneladas de producción
x1 + x2 ≥ 4
Juntando todo, obtenemos el problema de programación lineal
Maximizar (4x1 + 3x2)
Sujeto a
3x1 + 4x2 ≤ 12
4x1 + 2x2 ≤ 8
x1 + x2 ≥ 4
x1, x2 ≥ 0
Ahora, podemos resolver el problema de progrmación lineal usando el método del simplex o el método de las dos fases si es necesario como hemos visto en las secciones de teoría. En este caso usarmos nuestro famoso calculador de problemas de programación lineal
simplex method calculator.
Colocamos cada uno de los pasos, primero introducimos el problema en el programa
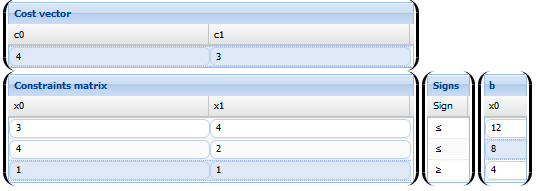
Paso 1:
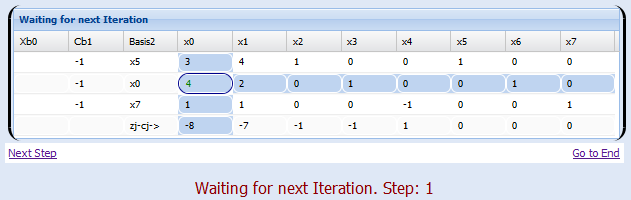
Paso 2:

Paso 3:
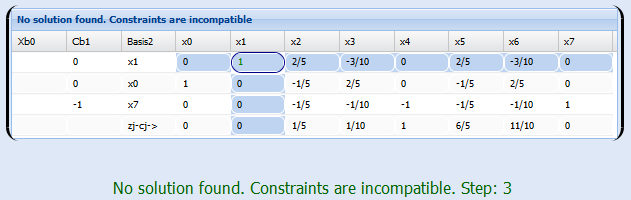
Como puede verse, el problema ha salido sin solulción óptima, esto es debido a que las restricciones son demasiado fuertes, la región factible es vacía.
Observe que si representamos gráficamente la región factible aparece el conjunto vacío, es decir, no se pueden satisfacer a la vez las tres restricciones.
Tendremos que alterar alguna (o varias) de nuestras restricciones para ello, hablamos con el dueño de la fábrica y le enviamos un email, diciendo que no es posible producir 4 Toneladas diarias de carbón y cumplir con todas estas restricciones, hay dos opciones
1) O relajamos nuestro objetivo ó
2) buscamos el método de relajar estas restricciones.
El jefe nos responde que había un error, y que el objetivo real es producir 3 Toneladas de Carbón. Introducimos este nuevo dato en nuestro problema de programación lineal, esto es, cambiamos la última de las restricciones por
x
1 + x
2 ≤ 3
Introducimos de nuevo el problema en
simplex method calculator y ahora sí, obtenemos

Así, hablamos con el jefe y le decimos que lo máximo que podemos producir con estas restricciones es
x1=1 Tn de lignito/día x2=2 Tn antracita/dia
Y esa es la solución de nuestro problema (modificado) de programación lineal. Alguna duda? ejecuta este problema
aquí o envíanos un
feedback.







