La fórmula integral de cauchy es tan importante que reservamos una sección completa dedicada a ella.
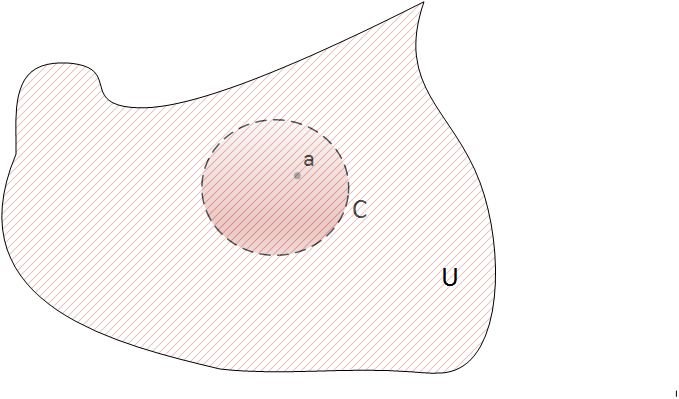
Dada f, una función holomorfa en un abierto U y sea a un punto del interior de U, entonces f es holomorfa en un disco que rodea al punto a. Si C es la frontera del disco entonces se cumple que
$$f(a) =\frac{1}{2\pi i}\ \int_{C} \frac{f(z)}{z-a}dz$$
Esta fórmula tan importante, expresa el valor de f en un punto en función de unos valores en la frontera de un disco que rodea al punto.
Su demostración, de la cual veremos una introducción, está basada en el Teorema de Cauchy para un abierto convexo:
Demostración de la fórmula integral de Cauchy
Como f es Holomorfa en todo U sea \(a \in U \). Para a se tiene:
\( \lim_{z \mapsto a} \frac{f(z)-f(a)}{z-a} = f'(a)\)
Así pues debe existir un cierto \( \epsilon > 0 \) para el cual se tenga si \( |z-a| < \delta \)
\( \frac{f(z)-f(a)}{z-a} - f'(a) < \epsilon \)
Entonces la función dada por
\( g(z)=\left\{\begin{matrix} \frac{f(z)-f(a)}{z-a} & z\ne a\\ f'(a) & z=a \end{matrix}\right. \)
Es contínua en todo U y holomorfa en todo U-{a}.
Su integral de línea en todo camino que rodee al punto a será cero ya que, por el
teorema3 de la seccíon integración compleja se tiene
\( \int_{C} g(z) dz = \int_{D(a, \epsilon)} g(z) dz \)
Como podemos tomar un radio tan pequeño como queramos y |g| está acotada superiormente por ser contínua en un compacto, se tiene que
\( \int_{D(a, \epsilon)} |g(z)| dz \le M 2\pi \epsilon \underset{\epsilon \rightarrow 0}{\rightarrow} 0 \)
Vale, ahora podemos tomar, para f
\( \int_{C} \frac{f(z)}{z-a} dz = \int_{C} \frac{f(z)-f(a)}{z-a} dz + \int_{C} \frac{f(a)}{z-a} = 0 + 2\pi if(a)\)
Eso era lo que queríamos demostrar.
La fórmula integral de Cauchy es notable también porque tiene importantes consecuencias, éstas son las que hacen única la rama del análisis de variable compleja.
Teorema 1: Infinita derivabilidad de una función Holomorfa
Dada f, una función holomorfa en un abierto U y sea a un punto del interior de U, entonces f tiene infinitas derivadas en a y se cumple que:
$$f^{(n)}(a) =\frac{n!}{2\pi i}\ \int_{C} \frac{f(z)}{(z-a)^{n+1}}dz$$
Observése que la esta fórmula contiene a la
fórmula integral de Cauchy si n=0, con 0!=1.
La demostración de este hecho se basa en que podamos introducir la derivada dentro del signo integral.
Teorema 2: Desigualdad de Cauchy
En las mismas condiciones del teorema anterior, sea M una constante positiva tal que para todo z de la curva C \( |f(z)| \le M \), entonces se tiene
$$|f^{(n)}(a)| \le \frac{M n!}{r^{n}}$$
El siguiente teorema debido a Liouville establece que no puede haber una funcion acotada y holomorfa en todo el plano complejo excepto si es constante.
Teorema 3: Terorema de Liouville
Si f es holomofa en todo el plano \( \mathbb{C} \) y f es acotada, es decir \( |f(z)| \le M \forall z \in \mathbb{C}\) entonces f es constante.
La demostración del teorema de Liouville es directa del teorema 2 tomando radios cada vez mas grandes.
Teorema 4: Terorema fundamental de álgebra
Sea \( P(z) = a_{0} + a_{1}x + ... + a_{n}x^{n} \) un polinomio con coeficientes complejos de grado mayor o igual que 1. Entonces P(z) tiene al menos una raiz en \( \mathbb{C} \).
Observese que en realidad tiene n raices ya que \( z_{0} \) es una raiz de P, entonces
\( P(z) = (z-z_{0})( b_{0} + b_{1}x + ... + b_{n-1}x^{n-1}) = (z-z_{0}) Q(z)\)
Así, se puede aplicar el teorema 4 a Q(z). Operando por inducción P(z) tiene n raices complejas.
Para demostrar el teorema 4, basta con considerar
\( f(z) = \frac{1}{P(z)} \)
Si P(z) no tuviera alguna raíz en \( \mathbb{C} \) entonces f(z) es
Holomorfa en todo \( \mathbb{C} \), entonces f debe estar acotada, por el teorema de Liuoville f es constante, entonces P(z) seria constante lo que es una contradicción.
Teorema 5: Princípio del módulo máximo
Si f es
Holomorfa sobre y en el interior de C, camino cerrado. Entonces el máximo de |f| ocurre sobre C.
Obsérvese que lo mismo puede aplicarse sobre el mínimo.
Teorema 6: Teorema del valor médio de Gauss
En las mismas condiciones que la
fórmula integral de Cauchy, se tiene
\( f(a) = \frac{1}{2\pi} \int_{0}^{2 \pi} f(a+re^{i\theta}) d\theta\)
La demostración de este hecho es facil, basta observar que en la
fórmula integral de Cauchy parametrizamos C, o sea
\( |z-a| = r \Rightarrow z= a + re^{i\theta} \).
Entonces la
fórmula integral de Cauchy se convierte en
\( f(a)= \frac{1}{2\pi i} \int_{0}^{2 \pi} \frac {f(a+re^{i\theta}) ir e^{i\theta} }{r e^{i\theta}} d\theta = \frac{1}{2\pi} \int_{0}^{2 \pi} f(a+re^{i\theta}) d\theta\)
Que era lo que queríamos demostrar.