We will see in this section a practical solution worked example in a typical maximize problem.
Sometimes it is hard to get to raise the linear programming, once done, we will use the methods studied in mathstools theory sections: Simplex, dual and two-phase methods.
We start with the statement of an optimization problem
Linear Programming problem
A mining company produces lignite and anthracite.
By the moment, it is able to sell all the coal produced, being the profit per ton of lignite and anthracite 4 and 3 monetary units, respectively.
Processing each ton of lignite requires 3 hours of coal cutting machine and another 4 hours for washing.
Also, the processing of one ton of anthracite required for same tasks 4 and 2 hours, respectively
The time available daily to each of these activities (cutting and washing) is 12 and 8 hours respectively.
Furthermore, it is desired to produce daily least 4 tons of coal.
1) Present the linear programming problem to determine the number of tons of lignite and anthracite to be produced daily in order to maximize gains.
2) Using the Simplex algorithm to solve the problem by the two phase method
We start understanding the problem. For this we construct the following tables
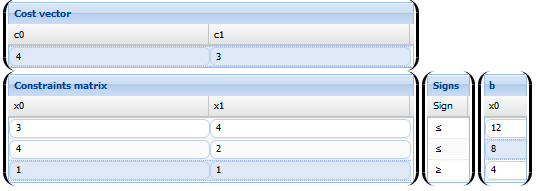
The first is the cost, or in this case, is a table of gains.
| Material | Gains produced
(monetary units /Tn) |
| Lignite | 4 |
| Anthracite | 3 |
| Material | Cutting hours (by Tn) | Washing time (by Tn) |
| Lignite | 3 | 4 |
| Anthracite | 4 | 2 |
Attached to this table, we have the constraint of time available for each machine daily
| Process | Hours available daily |
| Washing | 8 |
| Cutting | 12 |
and finally, we have the objective produce at least 4 tons of coal daily
With these data, we have what we need to pose the problem of linear programming.
We proceed as follows:
Lets
x1=Tons of lignite produced
x2=Tons of Anthracite produced
We want to maximize the gains, ie, maximize the function 4x1 +3 x2, this will be our objective function.
now building restrictions
We start with the washing process, note that for every day we have
3x1+ 4x2 ≤ 12
Since for every day the number of hours available washing is 12.
Analogously we have for the cutting process
4x1+ 2x2 ≤ 8
Because 8 is the number of hours available for the cutting machine.
Finally, the last of the restrictions is our goal tons of production
x1 + x2 ≥ 4
Putting it together, we obtain the linear programming problem
Maximize (4x1 + 3x2)
Subject to
3x1 + 4x2 ≤ 12
4x1 + 2x2 ≤ 8
x1 + x2 ≥ 4
x1, x2 ≥ 0
Now, we can solve the linear programming problem using the simplex or the two phase method if necessary as we have seen in sections of theory
In this case we use our famous calculator usarmos linear programming problems
simplex method calculator.
We placed each of the steps, first introduce the problem in the program
Step 1:
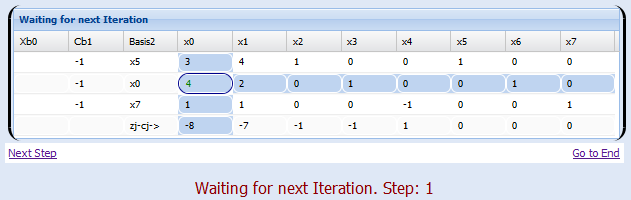
Step 2:

Step 3:
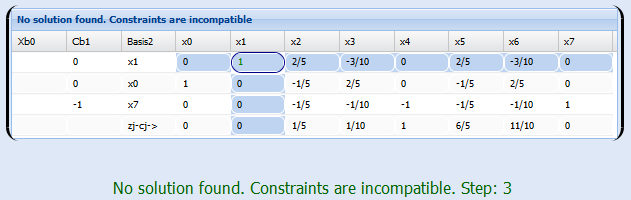
As can be seen, the output of method has gone unresolved optimal solution, this is because the restrictions are too strong, the feasible region is empty.
We will have to alter some (or more) of our restrictions for it, talk to the owner of the factory and send him an email, saying that it is not possible to produce 4 tons of coal daily and meet all these constraints, there are two options
1) Relax our objective function or
2) Relax constraints.
The chief replied that there was an error, and that the real goal is to produce 3 tons of coal (things that happens). We introduce this new information in our linear programming problem, that is, change the last of the restrictions
x
1 + x
2 ≤ 3
We introduce the problem again
simplex method calculator and now yes, we get

So, we talk again to the boss and say that the most we can produce with these restrictions is
x1=1 Tn de lignite/day x2=2 Tn Anthracite/day
And that is the solution of our linear programming problem (modified). Any Questions? run this problem
here or send us a
feedback.







