As we will see, in complex case, derivate concept is much stronger than real variable functions case.
In the real case case we want to remind that a function is differentiable at a point if all partial derivatives exist
and are continuous functions at that point.
The complex case is analogous, but it adds an extra condition: a system of partial differential equations called
Cauchy - Riemann equations
, must hold as well.
Cauchy - Riemann equations
Given a complex variable function:
$$ f: U \subset \mathbb{C} \mapsto \mathbb{C} $$
If complex derivate exists, f'(z) then
Cauchy - Riemann equations
defined as
\( u_{x} = v_{y}\)
\( u_{y} = -v_{x}\)
holds. In such case it is said that f is
Holomorphic
Complex derivate condition existence is very restrictive, as an example of this if we take the conjugate function
\( f(z) = \bar{z} \)
Take real and imaginary parts of f:
\(u(x, y)= x,\: v(x,y) = -y \)
Note that both functions have a good behavior (continuity, differentiability, ...), however, the function f has not complex derivative at any point because
Cauchy - Riemann equations never holds in any single point.
The previous example shows, as said that existence condition of a complex derivative is much stronger than in the case of real variable functions.
Anticipating the content of the following sections, when a function has a complex derivative at a point, then is also has derivatives of all orders
and therefore the function can be developed in power series around that point. That is the reason why we will adopt the term
Holomorphic for the function.
We want to highlight that many books use analytical term to refer to a complex function that has derivative.
All holomorphic function is analytical and reciprocally, all analytic function is Holomorphic, however, in complex analysis a function with a
single derivative is analytic, which does not occur in real variable. Therefore in my opinion the term holomorphic function is more appropriate
for the particular case of a complex variable function.
The complex derivate concept
Complex derivate f(x,y)= u(x,y) + iv(x,y) is defined as
$$f'(z)=\lim_{w \mapsto z } \frac{f(z)-f(w)}{z-w}$$
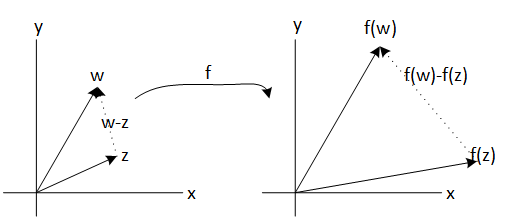
Lets see that the complex derivative is to take distance between f(z) and f(w), the distance between z and w calculate the quotient and then take the limit.
This is a geometric interpretation of the complex derivative.
Note that if we take directional derivatives, for instance if we approximate by the real part, we take
\(z=x+iy \)
\(w=x+h+iy\)
Then
\( f'(z)=\lim_{h \mapsto 0 } \frac{ u(x+h,y)+iv(x+h,y) - (u(x,y)+iv(x,y)) }{x+h+iy-(x+iy)} = \)
\( \frac{ u(x+h,y)-u(x,y) }{h} + i\frac{ v(x+h,y)-v(x,y) }{h}
= u_{x} + i v_{x} \)
On the other hand, if we approach by the imaginary side, that is, we take
\(z=x+iy\)
\(w=x+i(y+h)\)
We have
\( f'(z)=\lim_{h \mapsto 0 } \frac{ u(x,y+h)+iv(x,y+h) - (u(x,y)+iv(x,y)) }{x+i(y+h)-(x+iy)} \)
\( = \frac{ u(x,y+h)-u(x,y) }{ih} - i\frac{ v(x,y+h)-v(x,y) }{ih}
= v_{y} - i u_{y} \)
Note that these both force the condtion of
Cauchy - Riemann equations
.
Cauchy - Riemann equations
are a necessary condition for the complex derivative but not sufficient, the continuity of the partial derivatives of u and v must also be assumed.
As we see in the following theorem:
Converse of Cauchy - Riemann equations
Given two functions u (x, y) and v (x, y), such that verify the
Cauchy - Riemann equations
and with continuous partial derivatives in an open set \( U \subset \mathbb{C} \), then funcion:
$$f(x,y) = u(x,y) + iv(x,y)$$
has complex derivate \( \forall z \in U \)
Now it is enough to observe that if the derivative of f '(z) could also be calculated, that is, the second derivative of f (z), then the
Cauchy - Riemann equations
applied to f'(z), wich are
$$f'(z) = u_{x} +iv_{x}$$
Therefore
Cauchy - Riemann equations
applied to f' together with the equality of cross-partial derivatives:
$$u_{xx} = v_{xy} = (-u_{y})_{y} = - u_{yy}$$
$$ u_{xy} = - v_{xx} \Rightarrow -v_{xx} = (v_{y})_{y}$$
Then finally
$$ u_{xx} + u_{yy} = 0 $$
$$ v_{xx} + v_{yy} = 0 $$
Thus wehave that u(x,y) e v(x,y) are harmonic functions.
This shows the following theorem:
Harmonic functions
Given a function of complex variable whose derivative exists in an open set \( U \subset \mathbb{C} \). So the real part and the imaginary part are harmonic functions in
\( U \subset \mathbb{R}^{2} \), es decir \( \forall x \in U \) it is holds
$$ u_{xx} + u_{yy} = 0$$
$$ v_{xx} + v_{yy} = 0$$
Given a function of complex variable whose derivative exists in an open set \( U \subset \mathbb{C} \). Both real and imaginary parts are harmonic functions.
But there is still more than this: there is a kind of reciprocal that ensures that given an harmonic function u(x, y) there exists an harmonic conjugate v (x, y) such that
f(x,y) = u(x,y) + iv(x,y)
Is a complex
Holomorphic function variable.



