One of the most important ways to get involved in complex variable analysis is through complex integration. When we talk about complex integration we refer to the line integral.
Line integral definition begins with γ a differentiable curve such that
$$ \begin{matrix}\gamma : [a,b] \mapsto \mathbb{C}\\ \;\;\;\;\; \;\;\;\;\;\;\; x \mapsto \gamma(x) \end{matrix}$$
Now we split the interval [a, b] in n parts z
i such that z
0a, and
z
n=b
For each subinterval we take \( E_{i}=f(\zeta_{i})(z_{i}-z_{i-1}), \; i=1,..,n\).
Then we take partial sums \( \sum_{i=1}^{n}E_{i} = \sum_{i=1}^{n}f(\zeta_{i})(z_{i}-z_{i-1}) \). Making the limit when n tends to infinity we get the line integral as
$$\int_{a}^{b}f(z)dz \;\;, \;\; \int_{C}f(z)dz $$
Both two formulas are analogous
The complex integral over a C curve is defined as
\( \int_{C}f(z)dz = \int_{C}(u+iv)(dx+idy) \) \(= \int_{C}udx -vdy + i\int_{C}vdx -udy\).
A very interesting property of the integral and that is used in most of proofs and arguments is the follwing
$$\left | \int_{a}^{b }f(z)dz \right | \le \int_{a}^{b }\left |f(z) \right |dz$$
Click
here to see a proof of this fact.
Line integral definitionº
Given f, a complex variable function and γ a piecewise-differentiable curve. We define the line integral of f over γ as:
$$\int_{\gamma}f(z)dz = \int_{a}^{b}f(\gamma(t))\gamma'(t)dt $$
The most important therorem called
Cauchy's Theorem
which states that integral over a closed and simple curve is zero on simply connected domains. Cauchy gave a first demonstration by
supposing that function f has a continuous first derivative, later Eduard Gousart discovered that this hypothesis was actually redundant,
for this reason Cauchy's theorem is sometimes called Cauchy-Gousart's Theorem. This will be the version that we will see here.
In the following theorems, C is a closed and simple curve and contained in a simply connected open R region (this is a domain).
Theorem of Cauchy - Gousart
Given f a,
holomorphic function over R, then
$$\int_{C}f(z)dz = 0 $$
Click
here to see a proof of Cauchy's theorem.
Green's Theorem in the plane
Let P and Q be continuous functions and with continuous partial derivatives in R and on their boundary C. Then
\( \int_{C} P dx+ Q dy \) \(= \int\int_{R}[\frac{\partial Q}{\partial x}- \frac{\partial P}{\partial y}]dx dy \)
It is relatively simple to put Green's theorem in complex form:
Green's theorem in complex form
Given F, with continuous partial derivatives in R and on their boundary C. Then
\( \int_{C}F(z, \bar{z})dz \) \(= 2i\int\int_{R}\frac{\partial F}{\partial \bar{z}}dA \)
Click here to see a proof
Following Theorem is sometimes called reciprocal of the Cauchy's theorem:
Morera's Theorem
Given f, a complex variable function, lets suposse that it verifies
$$\int_{C}f(z)dz = 0 $$
then, f is
Holomorphic over R.
The following theorems are consequences of Cauchy's theorem
Theorem 1
If a and b are two points of R then the integral
$$ \int_{a}^{b} f(z) dz $$
It is independent of the path followed between a and b.
The proof of this theorem is simple, it is enough to observe if C is any path between a and b and C' is another different path, then for Cauchy's theorem,
the whole integral between C and C' is zero, as the path C 'does not matter, both line integrals are in fact equals.
Theorem 2
Lets a and b two points of R and F'(z) = f(z) then
$$ \int_{a}^{b} f(z) dz = F(b) - F(a) $$
Reciprocally, if a and z are points of R and it is fulfilled
$$ F(z) = \int_{a}^{z} f(z) dz $$
then, F is
Holomorphic in R and F'(z) = f(z)
The following theorem very important, it talk about that the value of an integral over a closed and simple curve that surrounds a singularity does not depend on the curve:
Theorem 3
Given f a function
Holomorphic
in a region bounded by two closed and simple curves C and C'
$$ \int_{C} f(z) dz = \int_{C'} f(z) dz$$
Where C and C' are traversed positively oriented, therefore counterclockwise.
The following theorem is an extension of the previous one to regions with n singularities instead two.

Figura 1: Region closed between curves C and C'
Teorema 4
Given f a function
Holomorphic
in a region bounded by nclosed and simple curves \( C_{1}, C_{2}, ..., C_{n}\). Which are enclosed by another larger curve C. Then.
\( \int_{C} f(z) dz = \int_{C_{1}} f(z) dz + \int_{C_{2}} f(z) dz + \) \( ... + \int_{C_{n}} f(z) dz \)
Where the curves curves \( C_{1}, C_{2}, ..., C_{n}\) are traversed positively oriented, that is, counterclockwise.
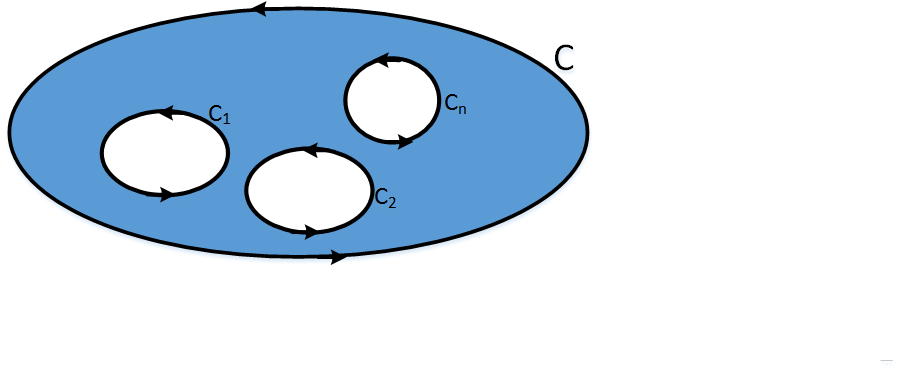
Figure 2: Region enclosed between C and \( C_{1}, C_{2}, ..., C_{n}\) curves.




