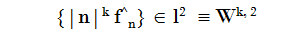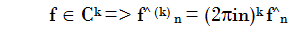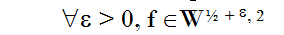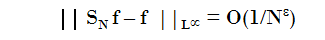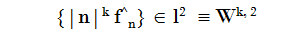Ya hemos visto en la teoría de los
espacios de Hilbert
que la clase de funciones L
2(T) se puede identificar con la clase de sucesiones l
2(Z)
mediante la transformada e Fourier, la cual es una aplicación isomorfa e isométrica entre estos espacios.
|
|
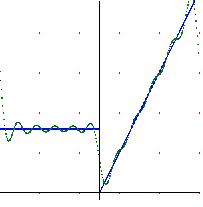
Convergencia de las series de Fourier al valor medio del salto en puntos con discontinuidades de salto.
|
Por tanto, para esta clase de funciones, la serie de Fourier es convergente es en el sentido de la norma generada por el
espacio de Hilbert, llamada de media cuadrática, es decir, obtuvimos
\( si \; f \in L^2(T) => ||S_N(x) - f(x)|| \to \ 0 \; cuando \; N \to \infty \)
Pero es importante resaltar que esta convergencia es en el sentido de la norma \(L^2(T)\) donde
\( ||f||_2 =(\int_{-0}^{1}|f(x)|^2dx)^\frac{1}{2} \)
Aún más, obtuvimos que dada una sucesión \( \{u_n\} \)del espacio
\( l^2(\mathbb{Z})=\{\{{a_n}\}_{n=0} ^{\infty} : \sum_{n=0}^{\infty}(a_n)^2<\infty\} \)
Existe una función de nuestro espacio de funciones para la que u forma los coeficientes de Fourier y la serie trigonométrica formada por esos coeficientes,
converge a la función en el sentido de la norma \(L^2(T)\).
Queremos ahora extender un poco más este espacio de funciones y encontrar condiciones de convergencia puntual y uniforme de la serie de fourier.
Comenzamos con un teorema cuya demostración no es trivial:
Teorema
Sea M un espacio de Medida finita (p. e. un intervalo) si p < q entonces
\( p < q \Rightarrow L^q(M) \subset L^p(M) \)
Así se tiene que
\( L^1(T)\supset L^2(T) \supset L^3(T) \supset ... \)
Concretamente y para que los definición de Coeficientes de Fourier tengan sentido solo es necesario que la función esté en el espacio
\(L^1(T)\) ya que
\( si \; f \in L^1(T) => ||f||_1 = \int_{0}^{1}|f(x)| dx < \infty \)
Entonces
\( ||f_n||_1 = | \int_{0}^{1} f(x) e^{2\pi i nx} dx |\leqslant \int_{0}^{1} |f(x)|| e^{2\pi i nx}|dx = \)
\( = \int_{0}^{1}|f(x)|dx= ||f||_1 < \infty \)
Así los coeficientes de Fourier están bien definidos en este espacio.
Consideramos ahora el espacio normado de funciones E = (L
1(T), || f ||
1)
donde la norma es
\( ||f||_1 = \int_{0}^{1}|f(x)| dx \).
Se puede demostrar, aunque no lo haremos aquí, que E es espacio de Banach (normado y completo).
La idea es ahora proceder de manera parecida a como hicimos en el caso de la convergencia cuadrática, consideremos ahora el espacio de sucesiones:
\( l^{\infty}(\mathbb{Z})=\{ \{a_n\} : sup|a_n| < \infty\} \).
Y en él definimos la norma:
\( || \{a_n\} ||_{\infty } = sup|a_n| \)
El espacio que llamamos H así definido, se puede demostrar que también es un espacio de Banach.
Consideramos ahora la aplicación
\( \begin{matrix} T:L^1(T) \rightarrow & l^\infty (\mathbb{Z}) \\ \;\;\;\;\;\;\;\;\;\;\;\; f \rightarrow &\{f_n\} \end{matrix} \)
En este caso, se puede demostrar que la aplicación T, es lineal, contínua e inyectiva pero no sobreyectiva, como teníamos en el análogo del caso
de las funciones de cuadrado integrable, véase la sección sobre los
espacios de Hilbert. En aquel caso la aplicación análoga
era un isomorfismo isométrico, no es este el mismo caso.
Para ver eso solo es necesario el siguiente y conocidísimo lema:
Lema (Riemann - Lebesgue)
\( Sea \;\;\; f \in L^1(T), \;\;\; Entonces\)
\( \begin{matrix} f_n \rightarrow 0 \\ \;\;\; n \rightarrow \infty \end{matrix} \)
De donde se deduce facilmente que T no es sobreyectiva, por ejemplo basta tomar la sucesión
\( (1, 1, 1, ...) \in l^\infty (\mathbb{Z}) \)
Sin embargo, trivialmente no verifica el lema de Riemann-Lebesgue.
Teorema de convergencia puntual 1 (Criterio de Hölder)
Sea la función
\( f \in L^1(T) \)
Contínua a trozos, tal que satisface la
Condición de Hölder a la derecha y a la izquierda, entonces:
\( S_Nf(x_0) \rightarrow \frac{f(x_0^+) - f(x_0^-)}{2} \)
Donde, \( f(x_0^+), f(x_0^-) \) son los límites a derecha y a izquierda respectivamente.
Por tanto, podemos decir que la serie de fourier en un punto converge puntualmente a mitad de la diferencia de los límites laterales a la función en ese punto.
El siguiente es un teorema parecido, solo que la condición de Dini es un poco más débil que la
condición de Hölder
Teorema de convergencia puntual 2 (Criterio de Dini)
Sea la función \( f \in L^1(T) \)
Y sea \(x_0 \in T \) cumpliendo
\( \int_{-\pi}^{\pi} \frac{f(x_0-y) -f(x_0)}{y} dx < \infty \)
Entonces
\( S_Nf(x_0) \rightarrow f(x_0) \)
Observación 1: las funciones diferenciables verifican trivialmente la condición de Hölder y de Dini ya que
\( \frac{f(x+h) -f(x)}{h} < C_d h, \;\; \forall h : 0 < h < \delta \)
Así, si es f diferenciable, la serie de Fourier de f, converge puntualmente.
Observación 2: Tambien esta función cumple la condición de Hölder aunque no es derivable
 Observación 3:
Observación 3: existen \( f \in L^1(T) \) tales que su serie de Fourier diverge en casi todo punto.
Observación 4: Desde 1968 se sabe que si\( f \in L^p(T), \forall p >1 \) la serie de Fourier de f converge en casi todo punto, el resultado para p=2
fué probado por Carlesson en 1966).
A continuación, un teorema de conevergencia uniforme para las series de Fourier que afirma que su serie de Fourier converge uniformemente para
toda función diferenciable.
Teorema 1 de convergencia uniforme de las series de Fourier
Si tenemos \( f \in C^p(T), p \geq 1 \)
Entonces la serie de Fourier converge uniformemente y el ratio de convergencia es
\( ||S_Nf - f ||_\infty =O( \frac{1}{N^{k-\frac{1}{2}}}) \)
Finalmente veremos un teorema de convergencia uniforme en el marco de los
Espacios de Sobolev , este teorema nos provee un espacio de funciones intermédio en el que podemos preescindir de funciones contínuas o diferenciables, pero para poder entenderlo, vemos primero el siguiente lema que nos devuelve los coeficientes de Fourier de las derivadas de una función (obviamente, en caso que sea diferenciable) en función de los Coeficientes de Fourier:
Lema
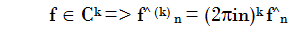
Teorema 2 de convergencia uniforme de las series de Fourier en términos del espacio de Sobolev
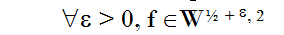
Entonces la Serie de Fourier de f converge Uniformemente con ratio de convergencia
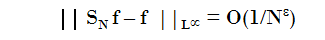
Lo que dice este importante Teorema si lo juntamos con el Lema anterior es que para que la serie de Fourier de una función sea uniformemente convergente solo es necesario que la función tenga solo un poco más de "média derivada".
En resumen, para que tengamos convergencia uniforme de la Serie de Fourier de una función, solo es necesario que