It is asked to calculate the Fourier series of following picewise function
\( f(x)=\left\{\begin{matrix} x & si\; x \in [-1,0)\\ 1 & si\; x \in [0, 1] \\ 0 & si\; |x|>1 \end{matrix}\right.\)
The first thing of all is to remember that our formulas here seen refer to interval \([-\pi, \pi] \), so we perform a change of variable
\(t = \pi x\) to obtain
\( f(t)=\left\{\begin{matrix} \frac{t}{\pi} & si\; t \in [-\pi,0)\\ 1 & si\; t \in [0, \pi] \\ 0 & si\; |t|>\pi \end{matrix}\right.\)
We can already apply our formulas for the Fourier series that we remember was
$$ f(x)=\frac{A_{0}}{2} + \sum_{n=1}^{\infty}(A_n cos nx + B_nsin nx ) $$
with \( A_i, B_i \in \mathbb{R} \) and
(1) \( A_0= \frac{1}{\pi} \int_{-\pi}^{\pi}f(x) dx\)
(2) \( A_n= \frac{1}{\pi} \int_{-\pi}^{\pi}f(x) cos nx dx\)
(3) \( B_n= \frac{1}{\pi} \int_{-\pi}^{\pi}f(x) sin nx dx\)
(1) \( A_0= \frac{1}{\pi} \int_{-\pi}^{\pi}f(x) dx\)
(2) \( A_n= \frac{1}{\pi} \int_{-\pi}^{\pi}f(x) cos nx dx\)
(3) \( B_n= \frac{1}{\pi} \int_{-\pi}^{\pi}f(x) sin nx dx\)
We start by calculating (1)
\( A_0=\frac{1}{\pi}\int_{-\pi}^{0} \frac{t}{\pi}dt + \frac{1}{\pi}\int_{0}^{\pi} dt = \frac{1}{\pi}( \pi-\frac{\pi}{2}) = \frac{1}{2} \)
The next, we calculate (2), for this our integral is separated into two pieces
\( A_n=\frac{1}{\pi}\int_{-\pi}^{0} \frac{t}{\pi} cos(nt)dt + \frac{1}{\pi}\int_{0}^{\pi} cos(nt)dt = I_1 + I_2\)
We start by calculating the first of the integrals I1, we do it by parts
\(\left\{\begin{matrix} u= \frac{t}{\pi} \Rightarrow du=\frac{dt}{\pi} \\ dv= cos(nt) dt \Rightarrow v=\frac{sin(nt)}{n} \end{matrix}\right.\)
Applying the method of integration by parts, whose formula we remember was
\(\int udv = uv-\int vdu\)
So
\( I_1 = 0 - \frac{1}{\pi^2} \int_{-\pi}^{0} \frac{sin(nt)}{n}dt = ... = \frac{1}{(\pi n)^2} (1-(-1)^n) \)
Now we calculate the second integral, we see that
\( I_2 = 0 \)
\( A_n= \frac{1}{(\pi n)^2} (1-(-1)^n) \)
Patience, it only remains to calculate the Bn, it is very similar to the previous calculation
\( b_n=\frac{1}{\pi}\int_{-\pi}^{0} \frac{t}{\pi} sin(nt)dt + \frac{1}{\pi}\int_{0}^{\pi} sin(nt)dt = J_1 + J_2\)
We start by calculating J1, we proceed as before by parts to obtain.
\( J_1 = -\frac{(-1)^n}{n\pi} \)
J2 is calculated directly
\( J_2 = \frac{1}{n \pi}(1- (-1)^n) \)
Therefore
\( B_n = \frac{2-(-1)^n}{n\pi}\)
We already have all the ingredients for the Fourier series formula, it is as follows
\(f(t)=\frac{1}{4}+\sum_{n=1}^{\infty}\frac{1}{(\pi n)^2} (1-(-1)^n)cos(nt) + (\frac{2-(-1)^n}{n\pi}) sin(nt) \)
Almost everything is done, the only thing now is to undo the initial variable change to finally get:
\( f(x)=\frac{1}{4}+\sum_{n=1}^{\infty}\frac{1}{(\pi n)^2} (1-(-1)^n)cos(n \pi x) + (\frac{2-(-1)^n}{n\pi}) sin(n \pi x) \)
To test our result we can go to Fourier Series calculator on this same site, if we introduce our function it remains
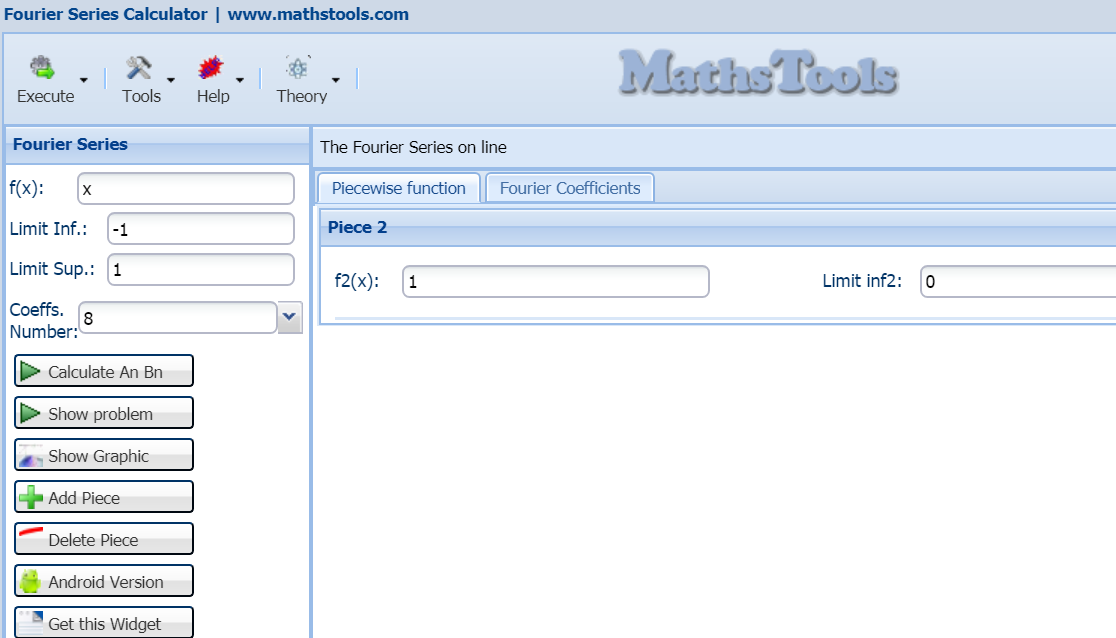
if we click on calculate, with 8 coefficients we obtain
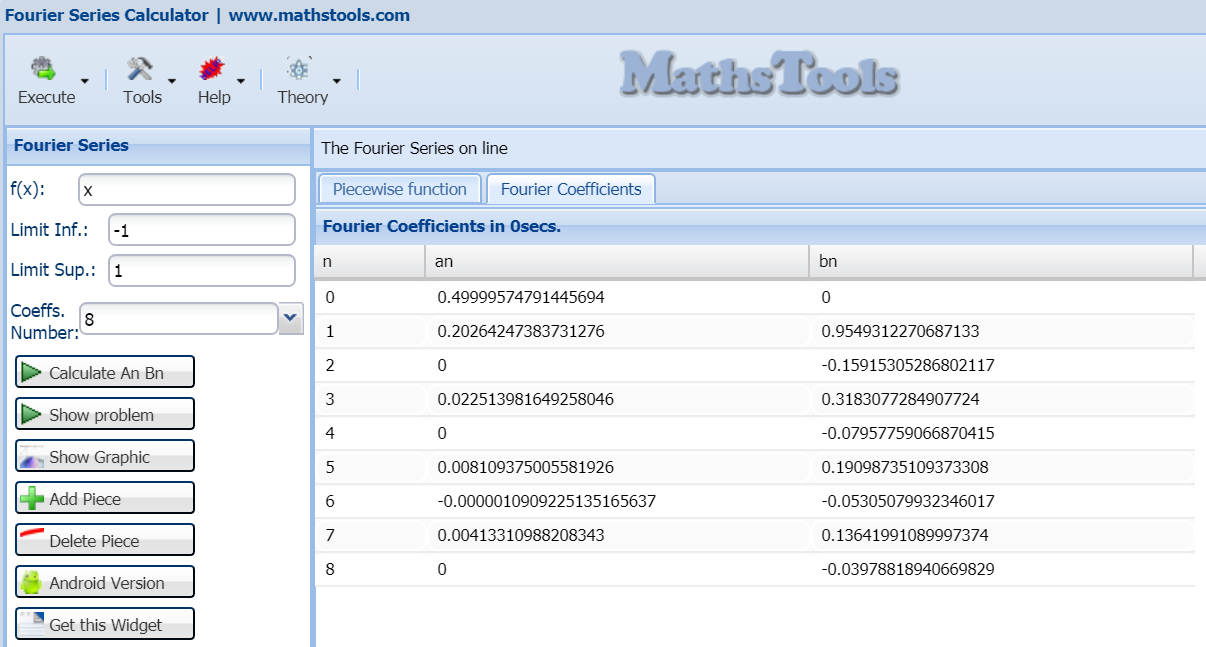
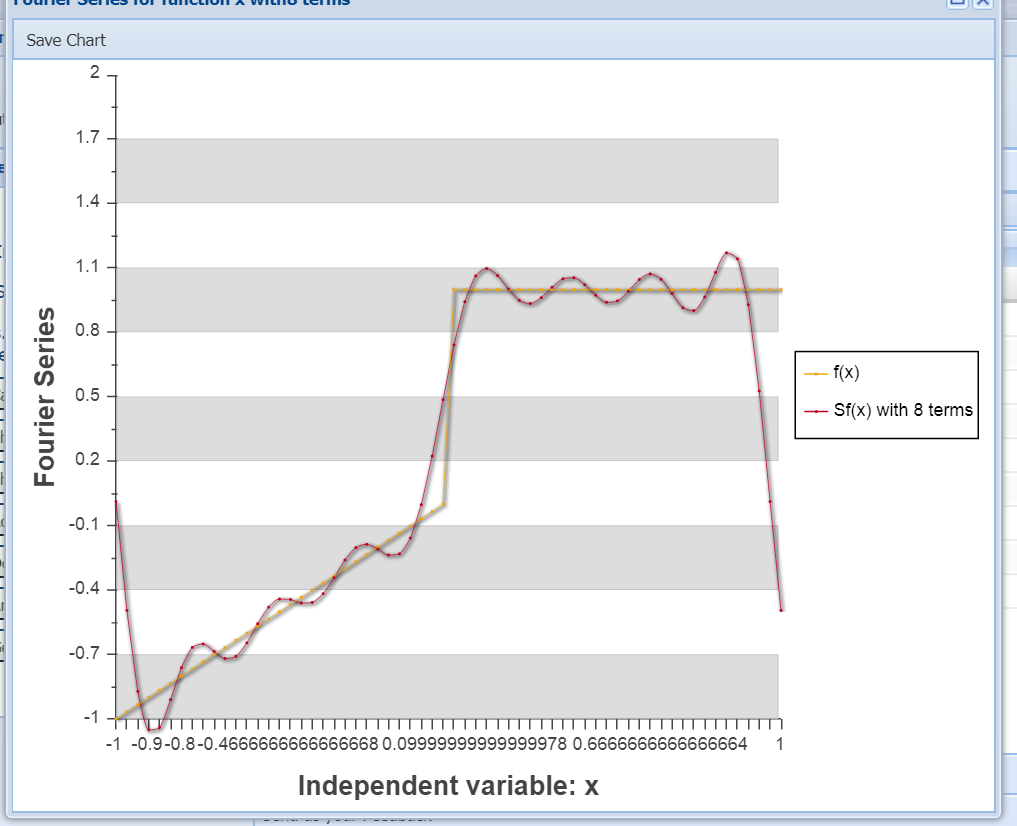
we see that numerical results coincide (except truncation error) with the obtained values, the graph of Fourier series remains