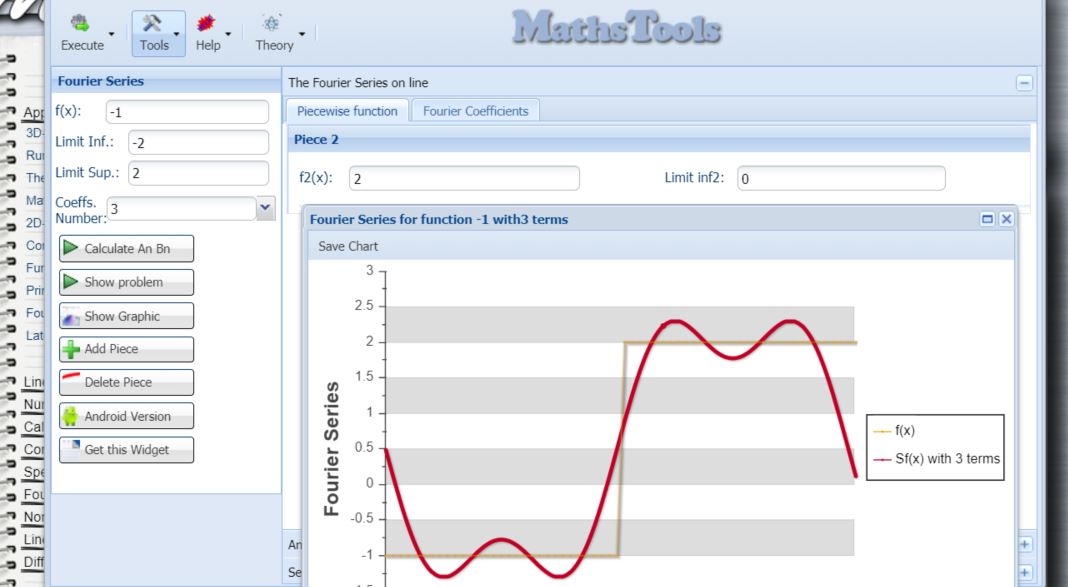
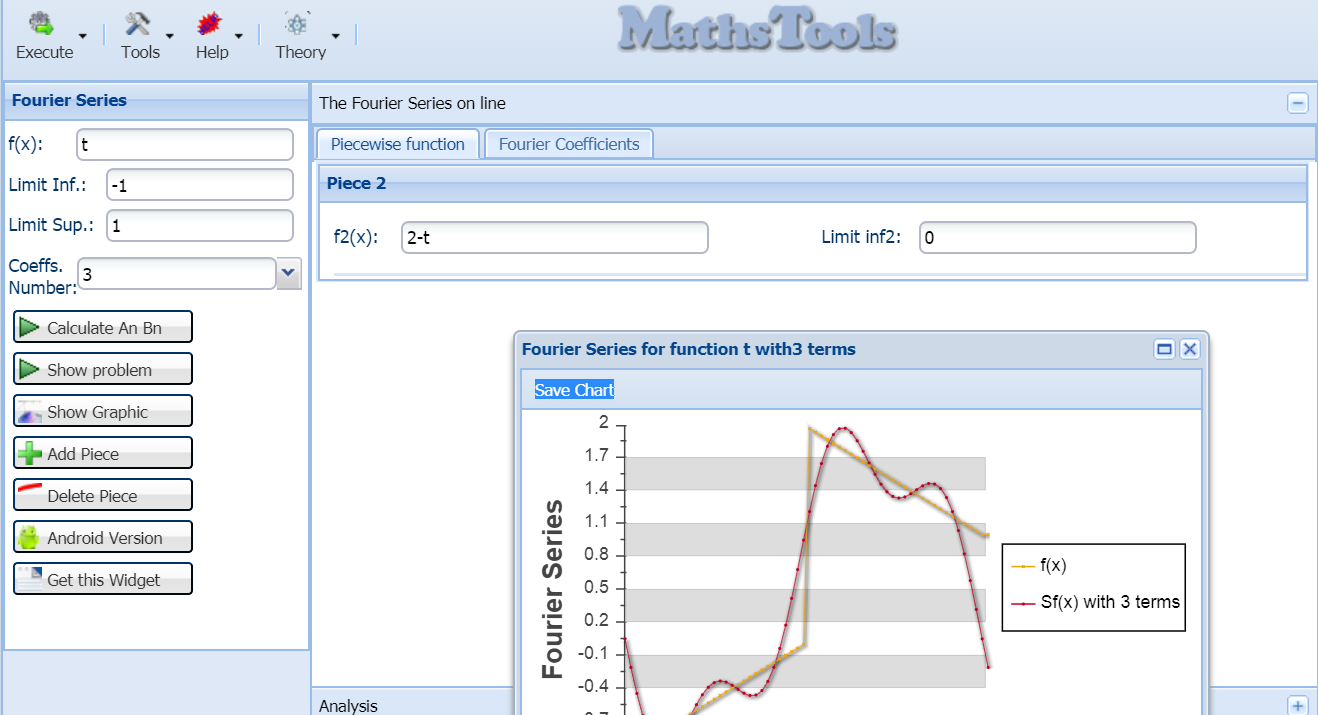
Inputs
Fourier Series Calculator allows you to enter picewise-functions defined up to 5 pieces, enter the following
0) Select the number of coefficients to calculate, in the combo box labeled "Select Coefs.Number".
1) Enter the lower integration limit (full range) in the field labeled "Limit Inf.".
2) Enter the upper integration limit (the total range) in the field labeled "Limit Sup.".
3) Enter the function of the variable x. Some examples are
if f(x) = e2x -> enter e^(2*x)
if f(x,y) = sin e2x -> enter sin(e^(2*x))
4) If the function is defined piecewise, enter the upper limit of the first interval in the field labeled "Sub-interval 1" and enter the function from that point to the next interval if more or "Limit inf." value entered in step 2)
5)If there are more pieces enter the upper end of the next subinterval in the field labeled "Sub-interval 2", and enter the function from that point to the next interval if more or "Limit inf." value entered in step 2)
6)If more pieces repeat the previous step in the following fields, Fourier Series Calculator lets you enter up to 4 subintervals.
Fourier Series Calculator Outputs
To calculate the coefficients of the Fourier series click "Fourier Series": After a few seconds, a window opens showing the An and An Fourier series coefficients for the function introduced, also will show some statistics of the calculations.
Click on "Show Graph" if you want to see the graphic representation of the function and the previously calculated series
Push in "df(x)/dx" To obtain the analytical derivative of the function
Push inn "Integral[a, b]" To obtain the primitive of the function in the interval introduced
Final Comments
Fourier Series Calculator has, in the precision limitation in calculations up to 16 decimal digits. Note that the precision in the calculation of each coefficient depends on size of interval entered, for an interval of length 2π the error is roughly o(10-7).
At same time, the maximum processing time is 20 seconds, after that time if no solution is found, Fourier Series Calculator will stop the execution, for higher execution times please use the applet on this website.
Fourier Series Calculator does not require installation of any kind, just a browser with javascript support.