|
|
Fourier series convergence to the midjump-value in jump-discontinuities points.
|
We will see in this section the behavior of the Fourier series for those functions with jump-discontinuities.
Exactly, the Dirichlet theorem assures us that the jump discontinuities, the Fourier series converges to the middle value of jump.
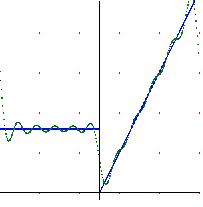
We also going to study the called Gibbs Phenomenon, which says that we are near a jump discontinuity, the Fourier series firing a 9% jump in the value of the jump.
Theorem (Dirichlet)
Let f be a continuous function except at a point \( x_0 \in [a, b]\).
Let's suppose that exits the lateral limits:
\( f(x_0^+)=\lim_{t\to 0^+} f(x_0+t)\)
and
\( f'(x_0^+)=\lim_{t\to 0^+} \frac{f(x_0+t) - f(x_0)}{t} \)
Then the Fourier series converges to the midpoint of the jump, wich means:
\( \lim_{N\to \infty}S_Nf(x_0) = \frac{f(x_0+t) - f(x_0)}{t} \)
We will now see the so-called Gibbs Phenomenon
Theorem (Gibbs Phenomenon)
Let f be as in the previous theorem, and \( S_Nf(x_0) \) its Fourier series at a point \( x_0 \in [a, b]\). Then it shoots with a value of approximately 9% of the value of the jump of
f, wich means:
$$ \lim_{t\to 0^+} \left [ \lim_{N\to \infty} (\sup_{x_0 \in (x, t)} S_Nf(x)) \right ] \cong S_Nf(x_0^+)+0.09(f(x_0^+)-f(x_0^-)) $$



