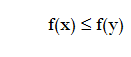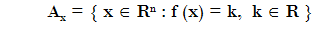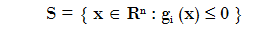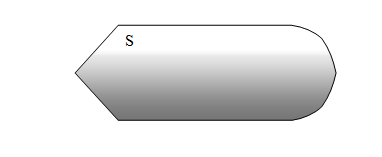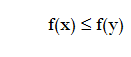Non Linear Programming

A non linear programming problem is a problem like The problem is very different than linear case where through linear algebra methods could solve the problem. In the nonlinear case our work will be much more complex and profound, it evokes concepts as "continuity" or "differentiability" and covers various fields of analysis.

In the case of our problem as the objective function f, such as the constraints are differentiable and have continuous second partial derivatives


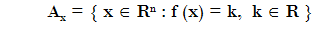
then issue may understand like a "special and extended" maximum or minimum value problem. Or a maximum or minimum restricted value problem.

Lets the feasible region


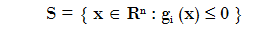
and lets the level sets of our function


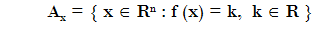
The feasible set of our problem is a set in the form

or it could adopt an unbounded form like

and the objetive-function level sets




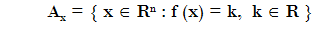
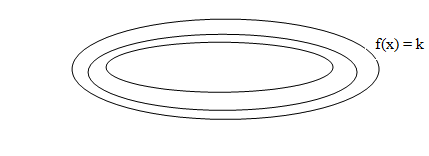
In general, the set constraints defines a region of R n .

We will make assumptions about this region (often topological) without paying much attention to the functions g i in themselves.

At first instance, we know that one Theorem that assures that every continuous function bounded in a compact (top and bottom).

This theorem together with the real numbers 13 axiom wich says that all real numbers set bounded above (below) has supperior (inferior) extreme.

This assures for us an existence of an optimum value for our problem in the bounded case.

Therefore, in the event that we have compactness in the constraints set we have an existence theorem and we can assure that there is a point and the feasible region S, such as for every x of S we have