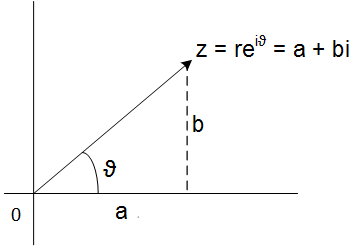Effectively, the equation
$$ x^{2} + 1 = 0 $$
Has solution, in fact it has two solutions wich are \( x = \pm \sqrt{-1} = \pm i \), the positive one is called as imaginary unit.
In general, numbers on the form
$$ z=a+bi $$
Are called complex numbers, a is called real part of z and b is imaginary part of z. They are denoted respectively for \( Re\,z=a, Im\,z=b \).
The complex plane consists of all complex numbers, that is, pairs of real numbers (a, b), formally
$$ \mathbb{C} = \{ z = a+bi : a, b \in \mathbb{R} \}$$
This notation, used for the first time by Euler in 1773, brought up a precious and prosperous branch of maths called Complex Variable analysis.
If we change the sign to the imaginary part we have the
conjugate complex . This is, the number
$$ \bar{z}=a-bi $$
It is called
conjugate complex .
Complex plane definition
Complex plane is defined as follows
$$ \mathbb{C} = \{ z = a+bi : a, b \in \mathbb{R} \}$$
and if \( z, w \in \mathbb{C} : z = a+bi, w = c + di \). There are addition and multiplication operations respectively are defined as:
$$ z+w = a+c +(b+d)i $$
$$ zw = (ac - bc) +(bc+ad)i $$
The complex plane endowed with these two operations has a Field structure.
Note that an attentive student could claim that \( \mathbb{C} = \mathbb{R} ^2 \), which is true from a topological point of view but not from the
algebraic one, because in the plane\( \mathbb{C} \) there are addition and multiplication operations which do not exist a at first in the usual
plane of \( \mathbb{R} ^2 \).
Every complex number can be written in what we call
polar form , like this
\(z = a+bi = re^{i\theta}\)
by
polar form of a complex number we have
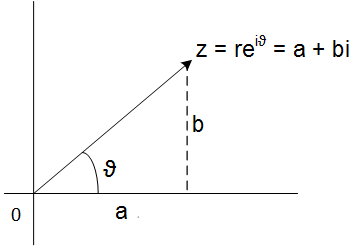
Figure 1: Polar form of complex number.
\(a=r \,cos\,\theta,\: b =r \,sin\,\theta\)
being r
modulus of z. It is calculated as
\(|z| = \sqrt{x^{2}+y^{2}} \)
The argument of a complex number is well defined except multiples of \(2\pi\), this is
$$ arg\, z = \theta + 2k\pi,\,\, k=1, 2, 3 ...$$
or
$$ arg\,z = \theta ,\,\,\,\ mod\,2\pi$$
We will refer, hereafter \(Arg z = \theta \), then
$$ arg\,z = Arg\,z + 2k\pi,\,\, k=1, 2, 3 ...$$
Suppose we want to calculate the square of z: , \(z^{2}\), then:
$$z = re^{i \theta} \Rightarrow z^{2} = r^2 e^{2i \theta} \Rightarrow arg z^{2} = 2 Arg\,z + 4k\pi,\,\, k=1, 2, 3 ...$$
When we do the reverse operation, the square root, it happens that
$$ arg \, z^{\frac{1}{2}} = \frac{arg \, z }{2} + \frac{2k\pi}{2} $$
So, now we can calculate square roots of negative numbers, for example, to calculate the square root of -1
$$ arg \, (-1)^{\frac{1}{2}} = \frac{\pi}{2} + k\pi $$.
because of this i and -i are both square roots of -1.
Complex numbers operations
Given two complex numbers
\( z_{1} = r_{1} e^{i \theta_{1} }\)
\( z_{2} = r_{2} e^{i \theta_{2} }\)
It is easy
\(arg\, z_{1}z_{2} = arg\, z_{1} + arg\,z_{2}\)
\(arg\, \frac{z_{1}}{z_{2}} = arg\, z_{1} - arg\,z_{2}\)
this is because
\( z_{1}z_{2} = r_{1} e^{i \theta_{1} } . r_{2} e^{i \theta_{2} } = r_{1} r_{2} e^{i (\theta_{1}+ \theta_{2}) } \)
Lets use this link to see how to calculate power and other operations on complex numbers.