Como veremos, en el caso complejo, la noción de derivada es mucho más fuerte que el caso de funciones de variable real. En este último caso, una función es diferenciable en un punto si existen las derivadas parciales y son funciones continuas en ese punto.
El caso complejo es igual, pero añade una condición extra: que se cumpla un sistema de ecuaciones en derivadas parciales llamado
Ecuaciones de Cauchy - Riemann
, concretamente
Ecuaciones de Cauchy - Riemann
Dada una función de variable compleja:
$$ f: U \subset \mathbb{C} \mapsto \mathbb{C} $$
Si existe la derivada compleja, f'(z) entonces se verifican las
Ecuaciones de Cauchy - Riemann
\( u_{x} = v_{y}\)
\( u_{y} = -v_{x}\)
En tal caso, se dice que la función f es
holomorfa
Esta condición de derivada compleja es bastante restrictiva, por ejemplo si tomamos el conjugado, es decir la función
\( f(z) = \bar{z} \)
Tomando las partes real e imaginaria de f
\(u(x, y)= x,\: v(x,y) = -y \)
Nótese que ambas tienen un buen comportamiento (continuidad, diferenciabilidad, ...), sin embargo, la funcion f no tiene derivada compleja en ningún punto pues nunca se verifican las
Ecuaciones de Cauchy - Riemann
para u y v.
El ejemplo anterior muestra que la condición de existencia de derivada compleja es mucho más fuerte que en caso de funciones de variable real. Anticipándonos al contenido de las secciones siguientes, cuando una función tiene derivada compleja en un punto, entonces existen las derivadas de todos los órdenes y por tanto la función es desarrollable en serie de potencias al rededor de ese punto. En cuyo caso adoptaremos el término de función
holomorfa
Queremos resaltar que en muchos libros, aparece el término analítica para referirse a una función compleja que tiene una derivada. Veamos, toda función holomorfa es analítica y reciprocamente, toda función analítica es Holomorfa, sin embargo,en variable compleja una función con una sola derivada ya es analítica, cosa que no ocurre en variable real, por eso en mi opinión, el término función holomorfa es más apropiado para el caso de particular de una función de variable compleja.
El concepto de derivada compleja
La derivada compleja de una función f(x,y)= u(x,y) + iv(x,y) se define como
$$f'(z)=\lim_{w \mapsto z } \frac{f(z)-f(w)}{z-w}$$
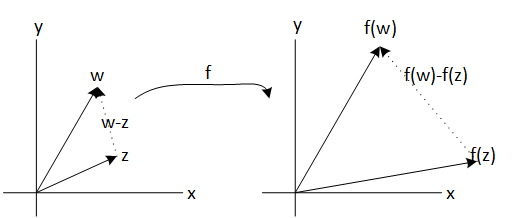
Véase que la derivada compleja es tomar el cociente entre la distancia entre f(z) y f(w), la distancia entre z y w y, despues hacer el límite. Esta es la interpretación geométrica de la derivada compleja.
Nótese que si tomamos derivadas direccionales, por ejemplo si nos aproximamos por la parte real, tomamos
\(z=x+iy \)
\(w=x+h+iy\)
Entonces
\( f'(z)=\lim_{h \mapsto 0 } \frac{ u(x+h,y)+iv(x+h,y) - (u(x,y)+iv(x,y)) }{x+h+iy-(x+iy)} = \)
\( \frac{ u(x+h,y)-u(x,y) }{h} + i\frac{ v(x+h,y)-v(x,y) }{h}
= u_{x} + i v_{x} \)
Por otro lado, si nos aproximamos por la parte imaginaria, o sea tomamos
\(z=x+iy\)
\(w=x+i(y+h)\)
Tenemos
\( f'(z)=\lim_{h \mapsto 0 } \frac{ u(x,y+h)+iv(x,y+h) - (u(x,y)+iv(x,y)) }{x+i(y+h)-(x+iy)} \)
\( = \frac{ u(x,y+h)-u(x,y) }{ih} - i\frac{ v(x,y+h)-v(x,y) }{ih}
= v_{y} - i u_{y} \)
Para que ambas sean iguales tienen que cumplirse necesariamente las
Ecuaciones de Cauchy - Riemann
Las
Ecuaciones de Cauchy - Riemann
son una condición necesaria para la derivada compleja, pero no son suficientes, debe suponerse también la continuidad de las derivadas parciales de u y v. como vemos en el siguiente teorema
Recíproco de las Ecuaciones de Cauchy - Riemann
Dadas dos funciones u(x,y) y v(x,y), tales que verifican las
Ecuaciones de Cauchy - Riemann
y con derivadas parciales contínuas en un conjunto abierto \( U \subset \mathbb{C} \), entonces la función:
$$f(x,y) = u(x,y) + iv(x,y)$$
Tiene derivada compleja \( \forall z \in U \)
Ahora bien, basta observar que si también se pudiera calcular la derivada de f'(z) o sea la derivada segunda de f(z) entonces también se cumplirían las
Ecuaciones de Cauchy - Riemann
para f'(z), es decir
$$f'(z) = u_{x} +iv_{x}$$
Se tiene, por las
Ecuaciones de Cauchy - Riemann
aplicadas a f' junto con la igualdad de las derivadas parciales cruzadas:
$$u_{xx} = v_{xy} = (-u_{y})_{y} = -u_{yy}$$
$$ u_{xy} = - v_{xx} \Rightarrow -v_{xx} = (v_{y})_{y}$$
Entonces, finalmente
$$ u_{xx} + u_{yy} = 0 $$
$$ v_{xx} + v_{yy} = 0 $$
Por tanto u(x,y) e v(x,y) son funciones armónicas.
Esto nos demuestra este teorema
Funciones armónicas
Dada una función de variable compleja cuya derivada existe en un conjunto abierto \( U \subset \mathbb{C} \). Entonces la parte real y la parte imaginaria son funciones armónicas en
\( U \subset \mathbb{R}^{2} \), es decir \( \forall x \in U \) se cumple
$$ u_{xx} + u_{yy} = 0$$
$$ v_{xx} + v_{yy} = 0$$
Dada una función de variable compleja cuya derivada existe en un intervalo abierto \( U \subset \mathbb{C} \). Entonces la parte real y la parte imaginaria son funciones armónicas
Pero aún hay más, hay una especie de recíproco que asegura que dada una función armónica u(x,y), entonces existe una conjugada armónica v(x,y) tal que
f(x,y) = u(x,y) + iv(x,y)
Es una función
holomorfa.



