Se pide calcular la serie de Fourier de la función a trozos
\( f(x)=\left\{\begin{matrix} x & si\; x \in [-1,0)\\ 1 & si\; x \in [0, 1] \\ 0 & si\; |x|>1 \end{matrix}\right.\)
Lo primero de todo es que nuestras fórmulas aquí vistas se refeiren a intervalo \([-\pi, \pi] \), así que hacemos un cambio de variable
\(t = \pi x\) y obtenemos
\( f(t)=\left\{\begin{matrix} \frac{t}{\pi} & si\; t \in [-\pi,0)\\ 1 & si\; t \in [0, \pi] \\ 0 & si\; |t|>\pi \end{matrix}\right.\)
Ya podemos aplicar nuestras fórmulas para la serie de Fourier que recordamos era
$$ f(x)=\frac{A_{0}}{2} + \sum_{n=1}^{\infty}(A_n cos nx + B_nsin nx ) $$
Con \( A_i, B_i \in \mathbb{R} \) y cumpliendo que
(1) \( A_0= \frac{1}{\pi} \int_{-\pi}^{\pi}f(x) dx\)
(2) \( A_n= \frac{1}{\pi} \int_{-\pi}^{\pi}f(x) cos nx dx\)
(3) \( B_n= \frac{1}{\pi} \int_{-\pi}^{\pi}f(x) sin nx dx\)
(1) \( A_0= \frac{1}{\pi} \int_{-\pi}^{\pi}f(x) dx\)
(2) \( A_n= \frac{1}{\pi} \int_{-\pi}^{\pi}f(x) cos nx dx\)
(3) \( B_n= \frac{1}{\pi} \int_{-\pi}^{\pi}f(x) sin nx dx\)
Empezamos calculando (1)
\( A_0=\frac{1}{\pi}\int_{-\pi}^{0} \frac{t}{\pi}dt + \frac{1}{\pi}\int_{0}^{\pi} dt = \frac{1}{\pi}( \pi-\frac{\pi}{2}) = \frac{1}{2} \)
A continuación, calculamos (2), para ello nuestra integral se separa en dos trozos
\( A_n=\frac{1}{\pi}\int_{-\pi}^{0} \frac{t}{\pi} cos(nt)dt + \frac{1}{\pi}\int_{0}^{\pi} cos(nt)dt = I_1 + I_2\)
Empezamos calculando la primera de las integrales I1, lo hacemos por partes
\(\left\{\begin{matrix} u= \frac{t}{\pi} \Rightarrow du=\frac{dt}{\pi} \\ dv= cos(nt) dt \Rightarrow v=\frac{sin(nt)}{n} \end{matrix}\right.\)
Aplicando el método de integración por partes, cuya fórmula recordamos era
\(\int udv = uv-\int vdu\)
Así
\( I_1 = 0 - \frac{1}{\pi^2} \int_{-\pi}^{0} \frac{sin(nt)}{n}dt = ... = \frac{1}{(\pi n)^2} (1-(-1)^n) \)
Ahora calculamos la segunda integral, vemos que
\( I_2 = 0 \)
\( A_n= \frac{1}{(\pi n)^2} (1-(-1)^n) \)
Paciencia, ya solo queda calcular los Bn, cuyo cálculo es muy parecido al cálculo anterior
\( B_n=\frac{1}{\pi}\int_{-\pi}^{0} \frac{t}{\pi} sin(nt)dt + \frac{1}{\pi}\int_{0}^{\pi} sin(nt)dt = J_1 + J_2\)
Empezamos calculando J1, procedemos como antes por partes para obtener.
\( J_1 = -\frac{(-1)^n}{n\pi} \)
J2 se calcula directamente
\( J_2 = \frac{1}{n \pi}(1- (-1)^n) \)
Por tanto
\( b_n = \frac{2-(-1)^n}{n\pi}\)
Ya tenemos todos los ingredientes para la fórmula de la serie de Fourier queda de la siguiente manera
\(f(t)=\frac{1}{4}+\sum_{n=1}^{\infty}\frac{1}{(\pi n)^2} (1-(-1)^n)cos(nt) + (\frac{2-(-1)^n}{n\pi}) sin(nt) \)
Ya está casi todo hecho, lo único ahora es deshacer el cambio de variable inicial para obtener finalmente:
\( f(x)=\frac{1}{4}+\sum_{n=1}^{\infty}\frac{1}{(\pi n)^2} (1-(-1)^n)cos(n \pi x) + (\frac{2-(-1)^n}{n\pi}) sin(n \pi x) \)
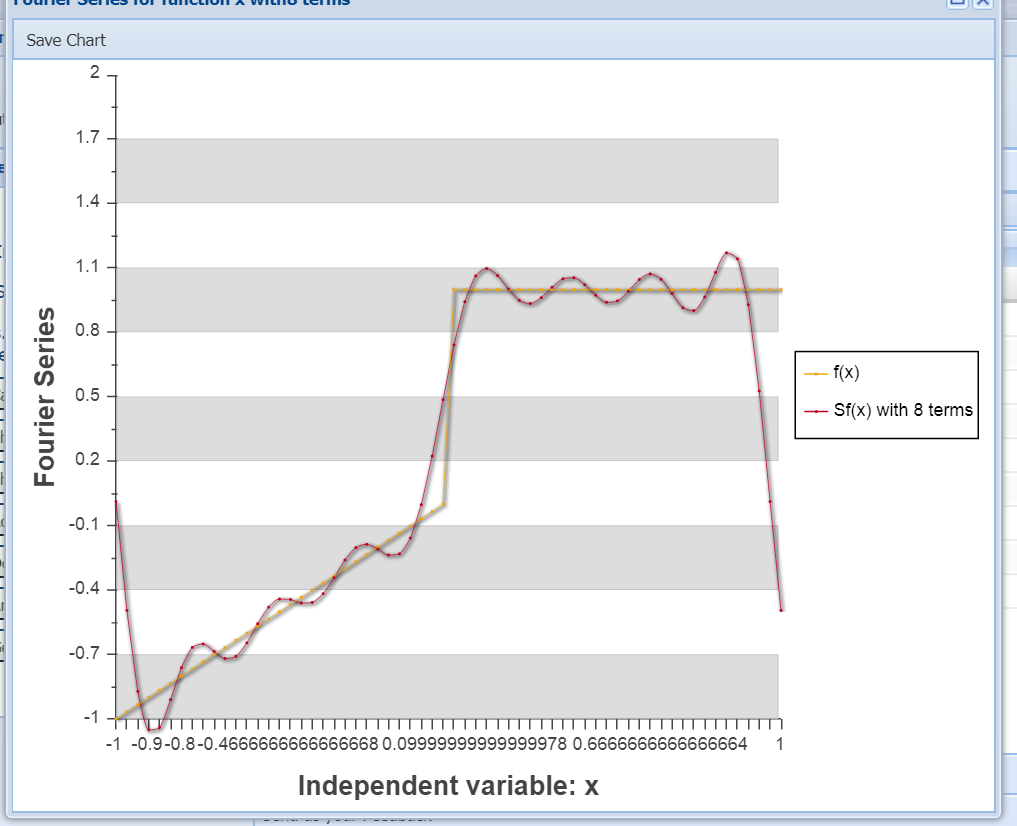
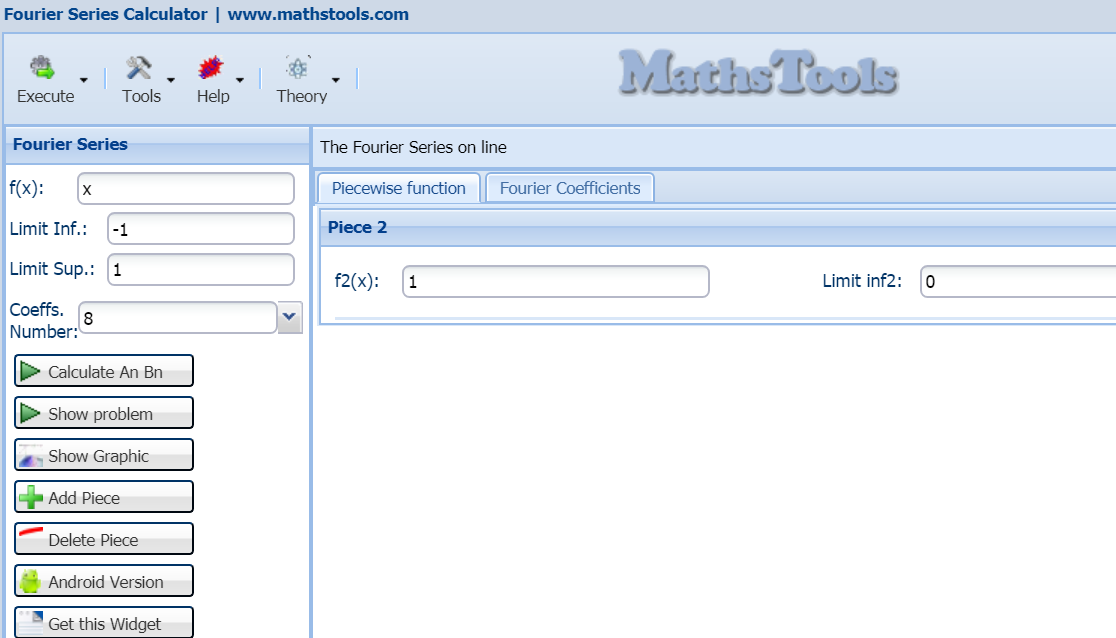
Para probar nuestro resultado podemos irnos al calculador de series de Fourier en esta misma página, si introducimos nuestra función queda
si pulsamos en calcular, con n=8 obtenemos
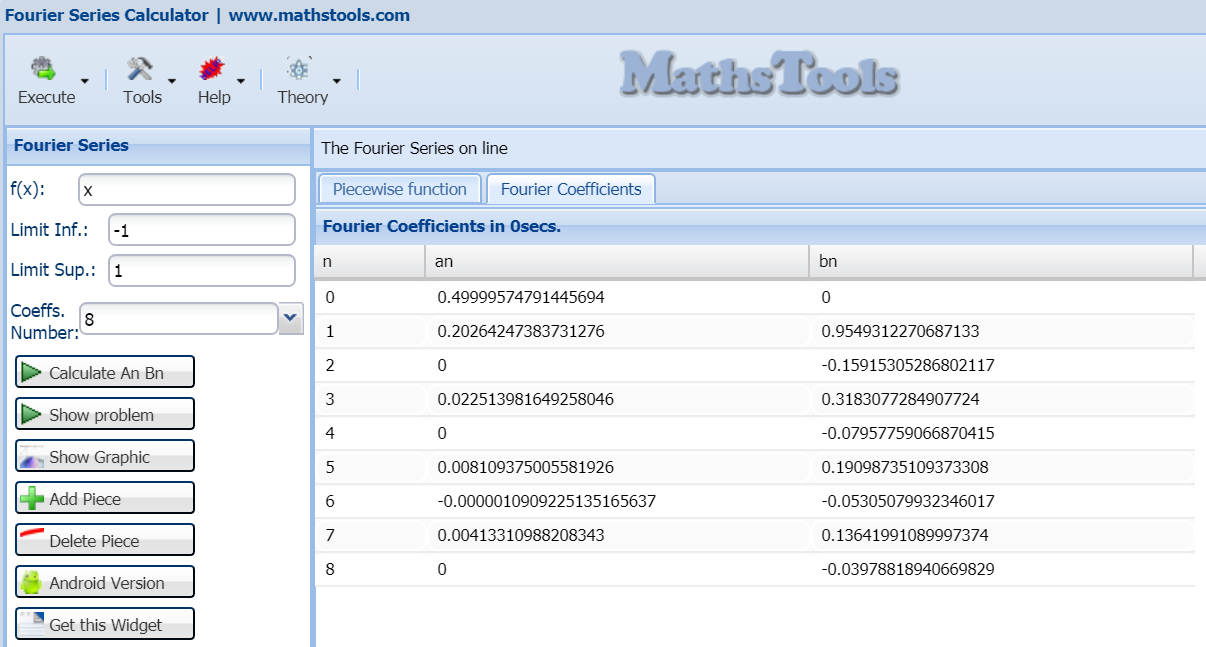
Como vemos los resultados numéricos coinciden (salvo error de truncación) con los valores obtenidos, la gráfica queda