|
|
Fourier series convergence to the midjump-value in jump-discontinuities points.
|
We will see at this section what is the behavior of the Fourier series for those functions with jump-discontinuities.
Exactly, the Dirichlet theorem assures us that the jump discontinuities, the Fourier series converges to the middle value of jump.
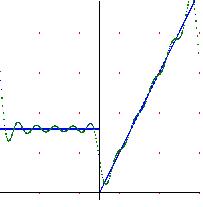
We also study the so-called Gibbs Phenomenon, which says that we are near a jump discontinuity, the Fourier series firing a 9% jump in the value of the jump.
Theorem (Dirichlet)
Let f be a continuous function except at a point
Suppose there exits
Then the Fourier series converges to the midpoint of the jump, ie
We will now see the so-called Gibbs Phenomenon
Theorem (Gibbs Phenomenon)
Let f be as in the previous theorem, then the Fourier series of f near of
It shoots with a value of approximately 9% of the value of the jump of f, ie
