We have already seen in theory of Hilbert spaces that there is a class of functions
L
2(T)
for which Fourier series are convergent. This convergence is in sense of the norm generated by this space,
called the quadratic norm, therefore we have obtained.
\( f \in L^2(T) \Leftrightarrow \lim_{N\rightarrow \infty}|| S_N(f) - f|| = 0 \)
|
|
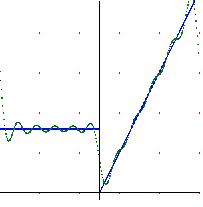
Fourier series convergence to the midjump-value in jump-discontinuities points.
|
But it is important to warn that this convergence is in the sense of the norm.
Moreover we have found that given a sequence {u} of elements in space
\(l^2(\mathbb{Z})= \{ \{ a_n\}_{n=-\infty}^{\infty} \, : \sum _{-\infty} ^{\infty} (a_n)^2 < \infty \)
There exists a function of our space of functions L
2(T) for which {u} are the Fourier coefficients
of trigonometric series, and it converges to the function in the norm sense of this space.
We now want to extend a little more this space of functions and find conditions for puntual and uniform convergence of Fourier series.
It is a fact, in a finite measure space M, as a closed interval, it can possible to shown that if p < q then
\(L^q(M)\subset L^p(M)\)
Actually, for definition of Fourier coefficients it is just necessary that the function be in the space L
1(T)
That is because if
\(f \in L^1(T) \int_{0}^{1}|f(x)|dx < \infty \) then:
\( ||f_n|| = |\int_{0}^{1}f(x) \, e^{2\pi inx} dx| \leq \int_{0}^{1} |f(x)| \, |e^{2\pi inx}| dx = \int_{0}^{1} |f(x)| dx = ||f|| _{L^1} \)
Thus the Fourier coefficients are well defined in this space.
Lets consider now the normed space of functions \( E=(L^1(T), \, ||f||_{L^1}) \), we mean that norm of f is defined as follows
\( ||f|| _{L^1} = \int_{0}^{1} |f(x)| dx \)
It is possible to show that E is actually a Banach space (normed and complete).
Lets consider now consider the sequence space
\( l^\infty (\mathbb{Z})= \{ \{ a_n\} \, : \sup |a_n| < \infty \} \)
ndice">n} : sup |a
n| < ∞}
We can define the normed space
\( H= (l^\infty (\mathbb{Z}), \, ||\{ a_n\}||_{\infty} \} \)
Where the norm is now
\( ||\{ a_n\}||_{\infty} = sup |a_n| \).
The space H so defined is also a Banach space.
We consider now the application
$$ \begin{matrix} T: L^1(T) \rightarrow l^\infty(\mathbb{Z}) \\ f \rightarrow \{f_n\} \end{matrix} $$
We mean the application applies to a function f its sequence of numbers. In this case, it can be shown that the application T, is linear,
continuous and injective but not surjective (as we had in the analog case of square integrable functions, see the section on Hilbert spaces).
To see that it is enough to see:
Lemma (Riemann - Lebesgue)
Given \( f \in L^1(T) \) Then:
$$ \lim_{n \mapsto\infty} \{f_n\} \mapsto 0 $$
From this it easy to follow that T is not surjective, for instance take the series
\( (1, 1,1..) \in l^\infty(\mathbb{Z}) \)
Theorem of punctually Convergence 1 (Hölder's Criterion)
Given a picewise-continuous function \( f \in L^1(T) \) such that satisfies
the
Right-left Hölder condition then
\( S_Nf(x_o)=\frac{f(x_0^+)+f(x_0^-)}{2}\)
where we are taking about lateral limits, for instance:
\( f(x_0^+)=\lim_{x\to x_0^+}f(x) \)
The following is a theorem is pretty similar, but Dini's condition is slightly weaker than
Hölder condition .
Theorem of punctually Convergence 1 (Dini's Criterion)
Let's be the function \( f \in L^1(T) \) and lets be
\(x_0 \in T:\int_{-\pi}^{\pi}|\frac{f(x_0-y)-f(x_0)}{y}|dx<\infty\)
then
\(S_Nf(x_0)\rightarrow f(x_0)\)
Observation 1: differentiable functions verified trivially both Hölder' and Dini's Criterion because:
\(\frac{f(x+h)-f(x)}{h}
Therefore we can state that if f differentiable then Fourier series of f converges punctually.
Observation 2: also a non-diferentiable function in some poits satifies the Hölder' and Dini's Criterion, as the following case:
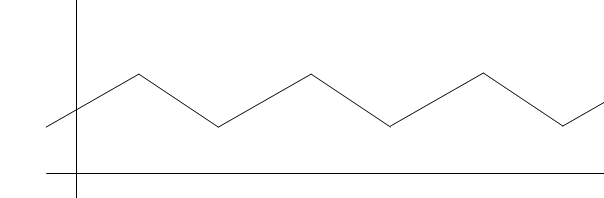Observation 3: There exist a function \( f \in L^1(T) \)
such that its Fourier series diverges almost everywhere
Observation 4: Since 1968 we know that if
\( f \in L^p(T), \forall p>1 \)
Fourier series of f converges almost everywhere (p = 2 is a Carlesson's result, shown in 1966, and generic p > 1 is a result from Richard Hunt in 1968).
Theorem 1: Uniformly convergence of Fourier series
If we have
\(f \in C^p(T), p \leq 1\)
Then the Fourier series converges uniformly and the convergence-ratio is
\(||S_Nf-f||_{L^\infty} = O( \frac{1}{N^{k-\frac{1}{2}} } ) \)
Finally we will see a uniform convergence theorem in the context of
Sobolev Spaces .
This theorem provides us with an intermediate function's space in which we can delete continuous or differentiable functions conditions,
but to understand it, we see first the following lemma which returns the Fourier coefficients of the derivatives of a function (obviously, if it's differentiable)
in terms of Fourier coefficients of function itself:
Lema
\( f \in c^k \Rightarrow \hat{f}^{(k)}_n = (2\pi in)^k\hat{f}_n \)
Theorem 2: uniformly convergence of Fourier Series in the context of Sobolev spaces
\( \forall \epsilon>0, \, f\in W^{\frac{1}{2}+\epsilon,2} \)
Then the Fourier series of f converges uniformly convergence with ratio
\(||S_Nf-f||_{L^\infty} = O( \frac{1}{N^{\epsilon} } ) \)
This important theorem join with the previous Lemma says that having uniformly convergency of the Fourier series is just necessary
the function to have jutst a little more than "half derivative".
Tu sum up, we have uniform convergence of Fourier Series of a function, it is only necessary:
\( \{ |n|^k \hat{f}_n\} \in l^2 \equiv W^{k,2} \)
