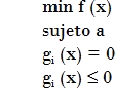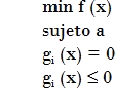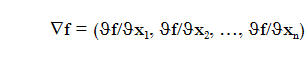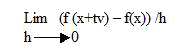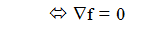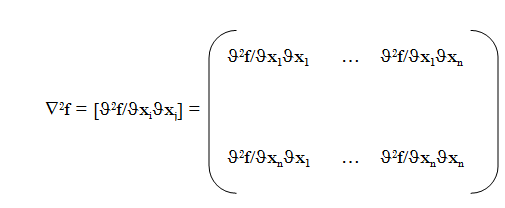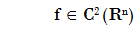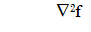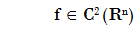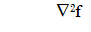Nos ocuparemos en esta sección de problemas del tipo
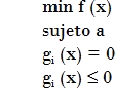
donde tanto la función objetivo como las funciones de restricciones son funciones
diferenciables.
como hemos dicho, el problema se puede plantear a algo a un problema extendido de máximos y mínimos.
Sea f continua y
diferenciable
El
gradiente de la función f se define como
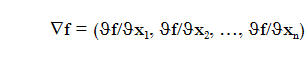
Que también denotaremos aquí como grad f(x).
Es decir, el gradiente es el vector formado por todas las derivadas de la función f.
A continuación vemos el concepto de derivada direccional, dicha derivada mide la tasa de cambio de la función en la dirección del vector
v.
Derivada direccional
Dado un vector v, se define la derivada de direccional de f en la direcciên v como
Df(x)v = df(x+tv)/dt, evaluado en t=0
También se puede definir como el límite
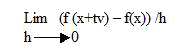
El siguiente Teorema nos asegura la existencia de todas las derivadas direccionales en el caso de funciones
diferenciables
Teorema (Existencia de derivadas direccionales en funciones diferenciables)
Sea

función diferenciable, entonces existen todas las derivadas direccionales, y la derivada en un punto x en la dirección v está dada por el producto escalar del Gradiente de f por v:
Df(x)v = <grad f(x) . v >
Como resultado de que la derivada direcciona mide la tasa de cambio de la función en la dirección de v. Esto es muy interesante en nuestro problema pues dado un punto, nos interesa saber en que dirección la función es creciente o decreciente y sobre todo en que dirección crece o decrece más rápido.
El siguiente problema responde a esta questión
Teorema
Si el grad f(x) ≠ 0, entonces grad f(x) apunta en la dirección de mayor crecimiento de la función
En otras palabras, si queremos saber en que dirección la función f, crece más rápidamente, tenemos que mirar en la dirección del vector grad f(x).
Análogamente, la dirección en la que la función decrece más deprisa es la de -grad f(x)
Esto nos da una idea de un algoritmo, dado un punto (x, f(x)), mediante los métodos de cálculo numérico podemos calcular el vector grad f(x) e iterar en esa dirección (en el sentido creciente o decreciente, según sea nuestro problema de maximizar o minimizar).
El siguiente Teorema nos habla de
extremos locales de funciones.
Teorema
Sea
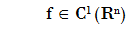
f tiene un
mínimo local en x, at x entonces ∇ f(x) = 0
Teorema (Relacción Mínimos - Convexidad)
Sea f como antes
f tiene un
mínimo local en x
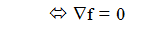
y f es
convexa en un entorno de x
Nota Se puede formular un teorema análogo con la relacción concavidad/Máximos locales
Ahora bien, dado un punto en el que grad f(x) = 0. Como saber si este punto es un máximo, un ménimo o un punto de silla? Lo que resta de sección trata de este asunto.
Si f es dos veces diferenciable, define la
matriz Hessiana de f
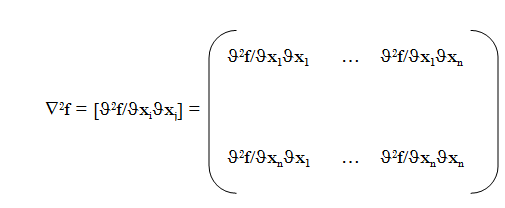
Teorema (Caracterización de extremos locales)
Sea
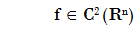
y sea x un punto en el cual grad f(x) = 0, entonces
a) Si la matriz Hessiana de f:
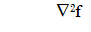
es
definida positiva entonces x es un mínimo local de f.
b) Si es
definida negativa entonces x es un méximo local de f.
c) Si no es ni definida positiva ni definida negativa, entonces x es un
punto de silla de f.
Teorema (Caracterización de convexidad por el Hessiano)
Sea
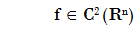
f es
convexa si y solo sí la matriz
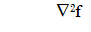
es definida positiva
Entonces si f es
convexa en toda la región S y tiene un
mínimo local en el punto x, entonces x es solución de nuestro Problema pues será un
mínimo global .
La convexidad de una función sólo asegura la continuidad de dicha función.
Por tanto no podemos hablar genéricamente del gradiente y menos aún de matriz Hessiana.
En lugar de eso, en la próxima sección definirimos el subgradiente, que hace el papel del gradiende
para funciones no
diferenciables (de echo, el subgradiente es el gradiente cuando la función es diferenciable)
Aquí ya podemos ver la complejidad de un problema de programación no-lineal. En el caso de funciones
convexas todo es mucho más sencillo ya que mínimos locales se convierten en mínimos globales.