X' (t) = f(X(t), t) ,
X(t0) = x0
Con
f: Rn x R → Rm
X: [a, b] ⊂ R → Rm
Nótese que el problema contiene un sistema de ecuaciones diferenciales con dimensión m.
A pesar de los numerosos métodos analíticos para resolver una ecuación (vectorial, o sistema de ecuaciones), en la práctica, es mayor el número de casos en los que dicho problema no se puede resolver analíticamente, bien porque la solución no pueda expresarse en términos de funciones elementales, o bien por dificultad técnica de encontrar la solución analítica.
En muchas ocasiones, se recurre a series de potencias, series de Fourier o a procesos infinitos de uno u otro tipo (series de potencias, fourier, aproximaciones, linealizaciones, etc ...) para intentar resolver el problema, al menos de un modo aproximado, en tales casos, suele ocurrir que la solución obtenida hace inviables los cálculos sobre un número finito pero muy grande de términos para poder obtener soluciones prácticas útiles.
Por eso se recurre a métodos numéricos, en su mayoría lineales que calculan soluciones aproximadas sobre discretizaciones del intervalo donde queremos que dichas soluciones estén definidas, los cálculos son tediosos, pero sencillos y fáciles de programar computacionalmente.
Por ejemplo, el problema
y' = y
y(0) = 1
Sabemos que admite la solución obvia y(x) = ex
Esto encierra el problema, al menos desde un punto de vista teórico. No obstante, supongamos que nos interesa saber su valor numérico valor en x = 10, tendríamos que recurrir a la calculadora o el computador para obtener que e10= 22026,466 .
La situación es peor aún en el caso que tengamos que integrar una función como
y(x) = ex/x
Cuya integral sabemos que no se puede escribir en términos de funciones elementales. En un caso como este habría que recurrir a las soluciones en series de potencias para hallar la solución analítica, sin embargo a la hora de obtener la solución numérica los cálculos serán inviables computacionalmente si queremos un cierto nivel de precisión.
También en el caso de ecuaciones no lineales, es muy complicado encontrar soluciones analíticas, por ejemplo en el caso del problema del péndulo simple
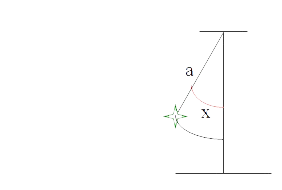
donde a, es la longitud de la cuerda rígida que sostiene el peso y x es el ángulo que forma la cuerda respecto a la vertical.
Aplicando las leyes de Newton al problema y operando, llegamos a que la ecuación diferencial que regula el movimiento del péndulo es
ay'' = - g sen x
siendo g la constante de aceleración de la gravedad para la tierra (mas o menos g = 9.8m/s) y a es, como queda dicho, la longitud de la cuerda o barra que sostiene al péndulo.
Dicha ecuación, se suele reducir al caso lineal suponiendo un movimiento pequeño del péndulo, ello permite sustituir sen x directamente por x. Este proceso permite hallar una solución analítica, pero ella solo será aproximada.
Es en estos casos donde los métodos numéricos presentados aquí se muestran particularmente útiles pues en ellos no tiene importancia la linealidad o no linealidad de la ecuación. No hay que olvidar, no obstante, que todos los problemas exigen un estudio analítico de las propiedades de las posibles soluciones, estabilidad del problema y de las condiciones iniciales, etc ...


