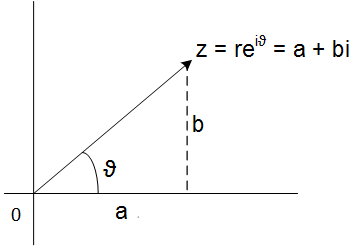Efectivamente, la ecuación
$$ x^{2} + 1 = 0 $$
Tiene solución, de hecho tiene dos las cuales son \( x = \pm \sqrt{-1} = \pm i \). De ellas, la raíz positiva recibe el nombre unidad imaginaria.
Números de la forma
$$ z=a+bi $$
Son llamados números complejos, a recibe el nombre de parte real de z y b es la parte imaginaria de z. Se denotan respectivamente por \( Re z=a, Im z=b \).
El plano complejo está formado por todos los números complejos, es decir pares de números reales (a,b), formalmente
$$ \mathbb{C} = \{ z = a+bi : a, b \in \mathbb{R} \}$$
Esta notación, usada por primera vez por Euler en 1773 da paso a una preciosa y próspera rama del análisis llamado análisis de Variable Compleja.
Si cambiamos el signo a la parte imaginaria tenemos el
conjugado de z . Es decir, al número
$$ \bar{z}=a-bi $$
Se le llama
conjugado de un número complejo .
Nótese que un estudiante atento podria reclamar que \( \mathbb{C} = \mathbb{R} ^2 \), lo cual es cierto desde un punto de vista topológico, pero no desde un punto de vista algebraico porque en el plano \( \mathbb{C} \) existen las operaciones suma y multiplicación las cuales no existen a priori en el plano usual de \( \mathbb{R} ^2 \).
Formalmente:
Definición de plano complejo
Se define el plano complejo como
$$ \mathbb{C} = \{ z = a+bi : a, b \in \mathbb{R} \}$$
y si \( z, w \in \mathbb{C} : z = a+bi, w = c + di \) entonces se definen las operaciones suma y multiplicación respectivamente como:
$$ z+w = a+c +(b+d)i $$
$$ zw = (ac - bc) +(bc+ad)i $$
El plano complejo dotado de estas dos operaciones tiene una estructura de cuerpo.
Todo número complejo puede ser escrito en la forma polar o también llamada
forma módulo-argumental: , así
\(z = a+bi = re^{i\theta}\)
y por la
forma polar de un número complejo, tenemos
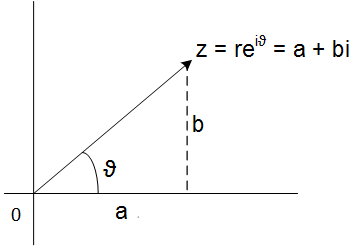
Figura 1: Forma polar de un número complejo.
\(a=r \,cos\,\theta,\: b =r \,sin\,\theta\)
Siendo r el
módulo de z que se calcula como
\(|z| = \sqrt{x^{2}+y^{2}} \)
El argumento de un número complejo está bien definido salvo múltiplos de \(2\pi\), o sea
$$ arg\, z = \theta + 2k\pi,\,\, k=1, 2, 3 ...$$
O bien
$$ arg\,z = \theta ,\,\,\,\ mod\,2\pi$$
Nos referiremos, a partir de ahora, a \(Arg z = \theta \), entonces
$$ arg\,z = Arg\,z + 2k\pi,\,\, k=1, 2, 3 ...$$
Supongamos que queremos calcular el cuadrado de z, o sea \(z^{2}\), entonces:
$$z = re^{i \theta} \Rightarrow z^{2} = r^2 e^{2i \theta} \Rightarrow arg z^{2} = 2 Arg\,z + 4k\pi,\,\, k=1, 2, 3 ...$$
Cuando hagamos la operación inversa, es decir, la raíz cuadrada, ocurre que
$$ arg \, z^{\frac{1}{2}} = \frac{arg \, z }{2} + \frac{2k\pi}{2} $$
Así, ahora podemos calcular raices cuadradas de números negativos, por ejemplo, para calcular la raiz cuadrada de -1
$$ arg \, (-1)^{\frac{1}{2}} = \frac{\pi}{2} + k\pi $$.
Por eso i y -i son ambas raizes cuadradas de -1.
Operaciones con números complejos
Dados dos números complejos
\( z_{1} = r_{1} e^{i \theta_{1} }\)
\( z_{2} = r_{2} e^{i \theta_{2} }\)
Es muy facil ver que
\(arg\, z_{1}z_{2} = arg\, z_{1} + arg\,z_{2}\)
\(arg\, \frac{z_{1}}{z_{2}} = arg\, z_{1} - arg\,z_{2}\)
Esto es sencillo de ver debido a que
\( z_{1}z_{2} = r_{1} e^{i \theta_{1} } . r_{2} e^{i \theta_{2} } = r_{1} r_{2} e^{i (\theta_{1}+ \theta_{2}) } \)
Para ver con se calculan potencias de números complejos
consulta este enlace .