Maximizar (x + 3y)
Sujeto a
x + y ≤ 3
x + y ≤ 2
x - y ≥ 1
x, y ≥ 0
Sujeto a
x + y ≤ 3
x + y ≤ 2
x - y ≥ 1
x, y ≥ 0
En este caso la región factible no es vacía y es acotada.
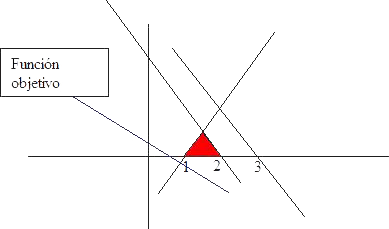
La función objetivo crece en el sentido de crecimiento de las coordenadas x e y. Por ser la región factible un conjunto convexo, la solución del problema se acanzará dentro del conjunto de puntos extremos de la región factible.
En este caso la solución será única, a simple vista se ve que el máximo se alcanza en el punto (3/2, 1/2) con valor óptimo 3 para la función objetivo.


