El Brusselator: ejemplo de Sistema de EDOS no lineal

El Brusselator es un problema oscilante para un cierto tipo de reacciones químicas modelizado por un sistema de ecuaciones diferenciales no lineales.

Consideremos el problema de valores iniciales

x' = 1-4x + yx2
y' = 3x - yx2

Con las condiciones iniciales
x(0) = 1.5
y(0) = 3.0

Vamos a utilizar la aplicación Runge-Kutta Calculator para resolver este problema numéricamente.

Si introducimos el problema en la aplicacion Runge-Kutta Calculator queda



Si ejecutamos la aplicación Runge-Kutta Calculator obtenemos el gráfico.



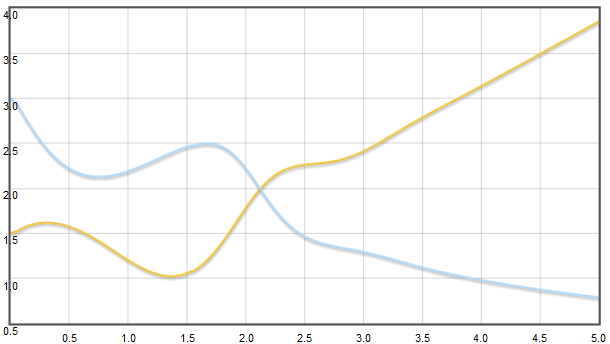
Obsérvese como, los valores para x e y producen una oscilacion antes de volverse inestables pasado cierto tiempo.

Ejecuta este problema con Runge-Kutta Calculator