Differentialble functions
Lets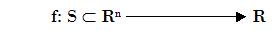
It is said that f is differentialble at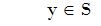
if there exists a vector
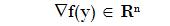
such us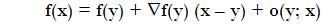
where 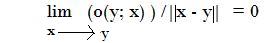
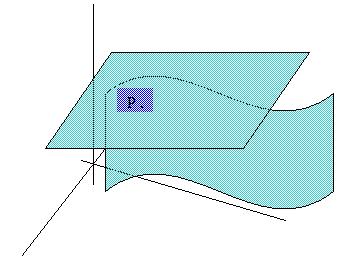
Differentiability definition refers that there exists a tangent space which is a "good aprox." to the function (exactly the aproximation has order one).
The existence of partial derivates does not guarantee differentiability, but a neccesary condition for differentiability at a point is the existence of all partial derivates of f and they are continuous at that point.
However, the converse is true: if a function is differentiable, then all partial derivates exist and are continuous at that point
Differentiability at a point can be understood as the function is "smooth" at that point, in the sense that it has no vertices and edges at this point


