La mayoria de las funciones de variable compleja son extensiones de las funciones de variable real. Por ejemplo,
el logaritmo complejo, cuyo cálculo se realiza con la fórmula
$$log z = log|z| + i Arg\,(z), \, Arg\,(z) = arg(z) + 2k\pi i$$
No es sino una extensión de su homóloga en variable real. Ahora podemos calcular logaritmos de números negativos o de otros números complejos en general.
Debido a que no podemos visualizar la gráfica de funciones de variable compleja como en el caso real, es interesante ver las funciones de variable compleja como transformaciones de ciertas regiones del plano. En nuestro ejemplo de
el logaritmo complejo, podemos ver como se transforma la circunferencia unidad, es decir el conjunto
$${z\in \mathbb{C} : |z|=1}$$
sabemos que su imagen mediante el log estará contenida en la recta imaginaria ya que
$${Re(log(z)) = 0 \,\,, \forall z \in \mathbb{C} : |z|=1}$$
además, sabemos que estará en el intervalo \([0,2\pi]\) del eje imaginario ya que
$${Im(log(z)) \in [0, 2\pi] 0 \,\,, \forall z \in \mathbb{C} : |z|=1}$$
Así la circunferencia unidad se transforma en el segmento \([0,2\pi]\) del eje imaginario.
Por tanto, es facil ver ahora que cualquier circunferencia de radio r se transforma en un segmento \(log(r)\,x \,[0,2\pi]\).
Y de ahí deducimos que todo el plano complejo se transforma en la banda dada por el conjunto
$${z\in \mathbb{C} : Im(z) \in [0, 2\pi]}$$
Obsérvese que la parte negativa de la banda es la imagen del interior de la circunferencia de radio uno y la parte positiva es la imagen del exterior, vea la siguiente figura:
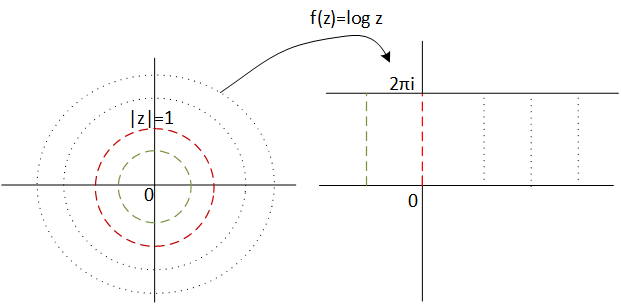
Figura1: tranformación del plano \( \mathbb{C}\) mediante el f(z)=log z.
Facil. ¿No? Esta es la idea: no podemos representar gráficas de funciones de variables compleja pero lo que si podemos es ver la geometria de su transformación.
Una aplicación se dice que es conforme cuando preserva los ángulos, es decir, f es conforme en z si dadas dos curvas regulares
$$\alpha: [a,b]\rightarrow \mathbb{C} $$
$$\beta: [c,d]\rightarrow \mathbb{C} $$
Entonce se tiene
$$\frac{\alpha'(z)}{\beta'(z)} = \frac{(f\circ \alpha)'(z)}{(f\circ \beta)'(z)}$$
Es decir, dadas dos curvas que se cortan en cierto punto z, el ángulo con el que los vectores tangentes de dichas curvas se cortan se conserva mediante la transformación f.
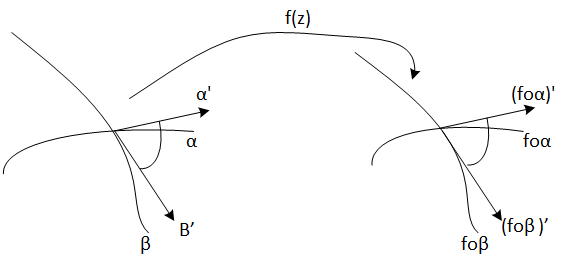
Figura 2: En una plicación conforme se conservan los ángulos.
Note que para que la definición anterior se cumpla se ha de cumplir en particular que \(f'(z) \neq 0 \).
Si la función es
holomorfa (es decir, tiene derivada compleja), entonces hay un teorema interesante llamado
Teorema de la aplicación conforme
Sea la función compleja
$$ f: U \subset \mathbb{C} \mapsto \mathbb{C} $$
Entonces f es conforme si y solo si, f es
holomorfa en todo U y \(f'(z) \neq 0 ,\,\,\forall z \in U \)
Por ejemplo, en el plano complejo la familia de rectas Imz = cte y la familia de rectas verticales Re(z)=cte, son ortogonales. El teorema de la aplicación conforme implica que la imagen de tales rectas mediante una función
holomorfa, seran sendas familias de curvas ortogonales.
Es interesante notar además que la funcion
holomorfa f(z)=w transforma "distancias cortas" en el plano z en "distancias cortas" en el plano w y el factor de aumento o de disminución viene dado por |f'(z)|.
El siguiente teorema nos garantiza que dada una región abierta, simplemente conexa, se puede transformar, mediante una aplicación
holomorfa en el disco unidad.
Teorema de la aplicación de Riemann
Sea C una curva cerrada y simple que es frontera de una región R. Sea ahora C' la circunferencia unidad que constituye la frontera de una región R' formada D((0,0), 1), o sea, por el disco de centro 0 y radio 1. Entonces existe F
holomorfa y biyectiva de R en R', además:
$$ \forall w \in C' \, \exists \, z \in C : w= F(z) $$
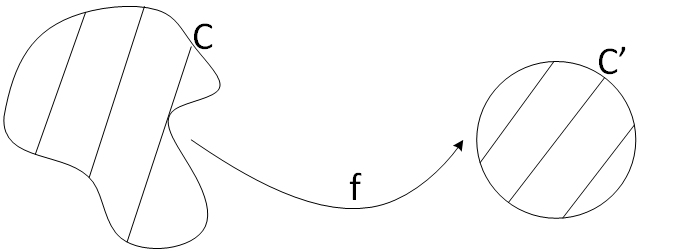
Figura 3: el teorema de la aplicación de Riemman.
O sea cualquier región con propiedades "dignas", es decir, simplemente conexa y limitada por una curva cerrada y simple, (por tanto acotada) puede aplicarse en el disco unidad mediante una aplicación
holomorfa.
Ejemplo
\(f(z)=\frac{1}{z} \)
Es facil ver que f "saca el interior del disco unidad" al exterior del disco y, al revés lo que está fuera del disco "lo mete" en el interior del disco.
No es tan facil ver que en realidad, f no es una inversión, es decir a cada punto z del interior del disco no le asigna un w del exterior tal que argumento de w = argumento de z y radio de w = inverso del radio de z. Es decir no es cierto que
\(arg \frac{1}{z} = arg z \)
Debido a la definición de
conjugado complejo, f primero obtiene el conjugado complejo de z y luego sí, obtiene el w en el mismo radio. Es decir, si que es cierto que
\(arg \frac{1}{z} = arg \bar z \)
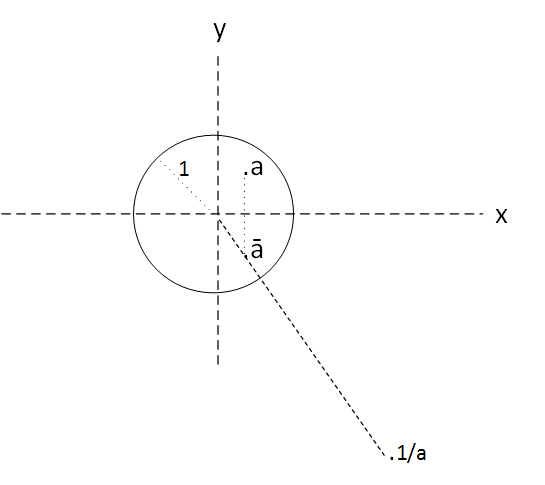
Figura 4: la función \(f(z)= \frac{1}{z}\).
Ejemplo
\(f(z)= z^{m}\)
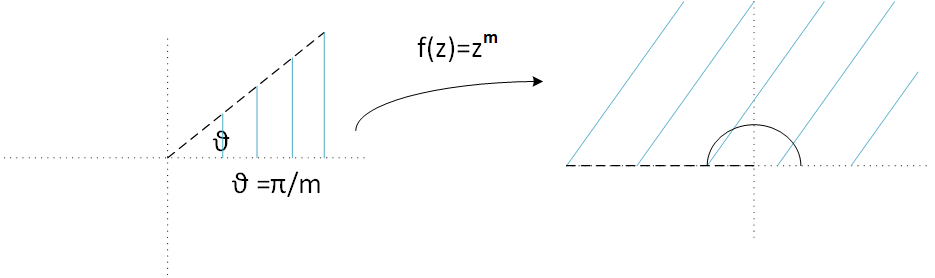
Figura 5: la función \(f(z)= z^{m}\).
En este caso la función f, transforma un sector del plano de ángulo \( \frac{\theta}{m} \) en el semiplano superior. Esto es debido a como
se transforman las
potencias de números complejos , cuya expresión es
$$z^{m} = |z|^{m} e^{(mi\theta +2mk\pi i)} $$.
Obsérvese que para elevar un número complejo a una potencia m, el argumento se multiplica por m (y el módulo se eleva a la potencia m).







