Otra de las maneras mas importantes de introducirse en el análisis de variable compleja es mediante la integración compleja. Cuando hablamos de integtración compleja nos referimos a la integral de línea.
La definición formal de integral de línea empieza con γ, una curva diferenciable tal que
$$ \begin{matrix}\gamma : [a,b] \mapsto \mathbb{C}\\ \;\;\;\;\; \;\;\;\;\;\;\; x \mapsto \gamma(x) \end{matrix}$$
Ahora, subdividimos el intervalo [a, b] en n partes z
i tal que z
0a, y
z
n=b
Para cada suintervalo tomamos \( E_{i}=f(\zeta_{i})(z_{i}-z_{i-1}), \; i=1,..,n\).
Ahora tomamos las sumas parciales \( \sum_{i=1}^{n}E_{i} = \sum_{i=1}^{n}f(\zeta_{i})(z_{i}-z_{i-1}) \). Haciendo el límite cuando n tiende a infinito obtenemos la integral de linea como
$$\int_{a}^{b}f(z)dz \;\;, \;\; \int_{C}f(z)dz $$
Las dos fórmulas son análogas
Separando parte real e imaginarias, la integral compleja sobre una curva C se define como
\( \int_{C}f(z)dz = \int_{C}(u+iv)(dx+idy)= \int_{C}udx -vdy + i\int_{C}vdx -udy \)
Una propiedad muy interesante de la integral y que se utiliza en numerosos argumentos es que
$$\left | \int_{a}^{b }f(z)dz \right | \le \int_{a}^{b }\left |f(z) \right |dz$$
Una demostración interesante puede
verse aquí .
Definición de integral de línea
Dada f, una función de variable compleja y γ una curva diferenciable a trozos se define su integral de línea de f sobre γ:
$$\int_{\gamma}f(z)dz = \int_{a}^{b}f(\gamma(t))\gamma'(t)dt $$
El teorema mas importante es el llamado
teorema de Cauchy
que establece que la integral a lo largo de una curva cerrada y simple es cero sobre dominios simplemente conexos. Cachy dió primero una demostración suponiendo que la función tiene una primera derivada contínua, mas tarde Eduard Gousart descubrió que en realidad, esta hipótesis era redundante, por esta razón el teorema de Cauchy se llama a veces Teorema de Cauchy-Gousart. Esta será la versión que veremos aquí.
En los siguientes teoremas, C será una curva cerrada y simple y contenida en una región R símplemente conexa.
Teorema de Cauchy - Gousart
Dada f, una función de variable compleja,
holomorfa en la región R, entonces
$$\int_{C}f(z)dz = 0 $$
Podemos ver
aquí una demostración del teorema de Cauchy.
Teorema de Green
Sean P y Q funciones contínuas y con primeras derivadas parciales contínuas en R y sobre su frontera C. Entonces
\( \int_{C} P dx+ Q dy \) \(= \int\int_{R}[\frac{\partial Q}{\partial x}- \frac{\partial P}{\partial y}]dx dy \)
Es relativamente sencillo poner el teorema de Green en forma compleja, la cual vemos a continuación
Teorema de Green - Forma compleja
Dada F, una función de variable compleja en la región R con derivadas parciales contínuas en R, entonces
\( \int_{C}F(z, \bar{z})dz \) \(= 2i\int\int_{R}\frac{\partial F}{\partial \bar{z}}dA \)
La demostración la podemos ver aquí
El siguiente Teorema es llamado a veces recíproco del teorema de Cauchy
Teorema de Morera
Dada f, una función de variable compleja en R, supongamos que se verifica
$$\int_{C}f(z)dz = 0 $$
Entonces, f es
holomorfa en R.
Los siguientes teoremas son consecuencias del teorema de Cauchy
Teorema 1
Si a y b son dos puntos de R entonces la integral
$$ \int_{a}^{b} f(z) dz $$
Es independiente del camino seguido entre a y b.
La demostración de este teorema es sencilla, basta observar si C es cualquier camino entre a y b y C' es otro camino distinto, entonces, por el teorema de Cauchy, la integral total entre C y C' será cero, como no importa el camino C', ambas integrales de línea serian iguales.
Teorema 2
Si a y b son dos puntos de R y F'(z) = f(z) entonces
$$ \int_{a}^{b} f(z) dz = F(b) - F(a) $$
Recíprocamente, si a y z son puntos de R y se cumple
$$ F(z) = \int_{a}^{z} f(z) dz $$
Entonces F es
holomorfa en R y F'(z) = f(z)
El siguiente teorema es muy importante, nos dice que el valor de una integral sobre una curva cerrada y simple que rodee una singularidad no depende de la curva.

Figura 1: Region encerrada entre las curvas C y C'
Teorema 3
Sea f una función
holomorfa en una región limitada por dos curvas cerradas y simples C y C'
$$ \int_{C} f(z) dz = \int_{C'} f(z) dz$$
Donde C y C' se recorren orientadas positivamente, es decir en sentido contrario a las agujas del reloj.
El siguiente teorema, es una generalización del anterior en una región con n singularidades.
Teorema 4
Sea f una función
holomorfa en una región limitada por curvas cerradas, disjuntas y simples \( C_{1}, C_{2}, ..., C_{n}\). Las cuales están encerradas por otra curva mayor C. Entonces.
\( \int_{C} f(z) dz = \int_{C_{1}} f(z) dz + \int_{C_{2}} f(z) dz + \) \( ... + \int_{C_{n}} f(z) dz \)
Donde las curvas \( C_{1}, C_{2}, ..., C_{n}\) se recorren orientadas positivamente, es decir en sentido contrario a las agujas del reloj.
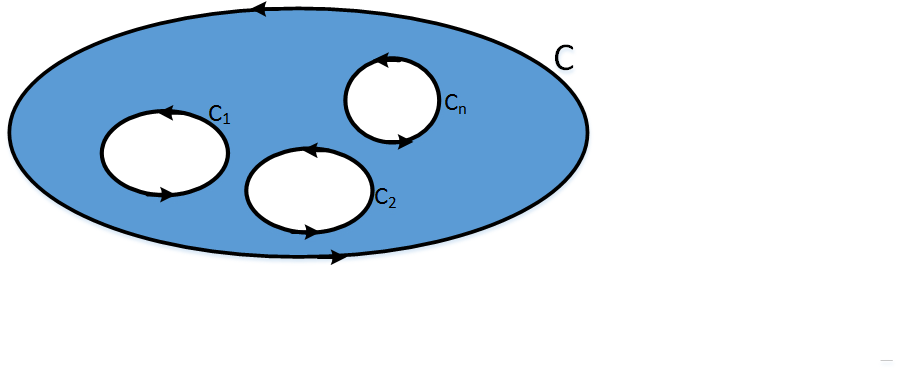
Figura 2: Region encerrada entre las curvas C y \( C_{1}, C_{2}, ..., C_{n}\)




